
分析 (Ⅰ)根据向量的数量积的运算和模的计算即可,
(Ⅱ)建立坐标系,得到则$\overrightarrow{c}$的轨迹为以(2,1)为圆心,以r=3为半径的圆,即可求出最大值.
解答 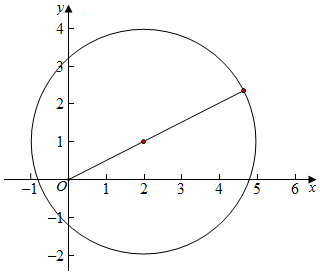 解:(Ⅰ)∵|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$•$\overrightarrow{b}$=0,
解:(Ⅰ)∵|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$•$\overrightarrow{b}$=0,
∴|$\overrightarrow{a}$-2$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+4|$\overrightarrow{b}$|2-4$\overrightarrow{a}$•$\overrightarrow{b}$=16+16-0=32,
∴|$\overrightarrow{a}$-2$\overrightarrow{b}$|=4$\sqrt{2}$
(Ⅱ)∵$\overrightarrow{a}$•$\overrightarrow{b}$=0,
∴$\overrightarrow{a}$⊥$\overrightarrow{b}$,
以$\overrightarrow{a}$所在的直线为x轴,$\overrightarrow{b}$所在的直线为y轴,建立坐标系,
∵|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=2,
∴$\overrightarrow{a}$=(4,0),$\overrightarrow{b}$=(0,2),
设$\overrightarrow{c}$的坐标为(x,y),
∴$\overrightarrow{c}$-$\overrightarrow{a}$=(x-4,y),$\overrightarrow{c}$-$\overrightarrow{b}$=(x,y-2),
∵($\overrightarrow{c}$-$\overrightarrow{a}$)•($\overrightarrow{c}$-$\overrightarrow{b}$)=0,
∴x(x-4)+y(y-2)=0,
即(x-2)2+(y-1)2=9,
则$\overrightarrow{c}$的轨迹为以(2,1)为圆心,以r=3为半径的圆,
圆心到原点的距离d=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
故|$\overrightarrow{c}$|最大值=d+r=3+$\sqrt{5}$
点评 本题考查平面向量数量积的运算,本题解题的关键是写出满足条件的对应的点,根据数形结合思想求出向量的模长.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
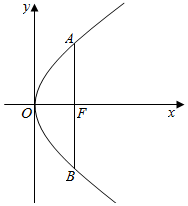 如图所示,已知抛物线C:y2=2px(p>0)的焦点为F,过点F垂直于x轴的直线与抛物线C相交于A,B两点,抛物线C在A,B两点处的切线及直线AB所围成的三角形面积为4.
如图所示,已知抛物线C:y2=2px(p>0)的焦点为F,过点F垂直于x轴的直线与抛物线C相交于A,B两点,抛物线C在A,B两点处的切线及直线AB所围成的三角形面积为4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,lg6] | B. | (-∞,3lg2] | C. | [lg6,+∞) | D. | [3lg2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60 | B. | 90 | C. | 150 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com