[题目]记集合A={(x.y)|x2+y2≤16}和集合B={(x.y)|x+y﹣4≤0.x≥0.y≥0}表示的平面区域分别为Ω1 . Ω2 . 若在区域Ω1内任取一点M(x.y).则点M落在区域Ω2的概率为．题目和参考答案——青夏教育精英家教网—

【题目】记集合A={（x，y）|x2+y2≤16}和集合B={（x，y）|x+y﹣4≤0，x≥0，y≥0}表示的平面区域分别为Ω1 ， Ω2 ，若在区域Ω1内任取一点M（x，y），则点M落在区域Ω2的概率为．

【答案】
【解析】解：由题意可得A表示圆心为原点半径为4的圆及其内部，
由圆的面积公式可得Ω1的面积S=π×42=16π，
集合B表示的平面区域为两直角边都为4的直角三角形，
∴由三角形的面积公式可得Ω2的面积S′= ×4×4=8，
∴点M落在区域Ω2的概率P= = ，
所以答案是：．
【考点精析】关于本题考查的几何概型，需要了解几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等才能得出正确答案．

练习册系列答案

创新设计高考总复习系列答案

魔法教程课本诠释与思维拓展训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥平面ABCD，AB=PA=1，AD= ，F是PB中点，E为BC上一点．

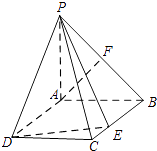
（1）求证：AF⊥平面PBC；
（2）当BE为何值时，二面角C﹣PE﹣D为45°．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在△ABC中，∠BAC=120°，AC=3，△ABC的面积等于，D为边长BC上一点．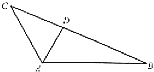

（1）求BC的长；
（2）当AD= 时，求cos∠CAD的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】（本小题满分14分）

设△ABC三个内角A、B、C所对的边分别为a，b，c. 已知C＝，acosA=bcosB．

（1）求角A的大小；

（2）如图，在△ABC的外角∠ACD内取一点P，使得PC＝2．过点P分别作直线CA、CD的垂线PM、PN，垂足分别是M、N．设∠PCA＝α，求PM＋PN的最大值及此时α的取值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】（本小题满分为16分）为了保护环境，发展低碳经济，某单位在国家科研部门的支持下，进行技术攻关，新上了把二氧化碳处理转化为一种可利用的化工产品的项目，经测算，该项目月处理成本y（元）与月处理量x（吨）之间的函数关系可近似地表示为：

，且每处理一吨二氧化碳得到可利用的化工产品价值为200元，若该项目不获利，国家将给予补偿．

（1）当x∈[200,300]时，判断该项目能否获利？如果获利，求出最大利润；如果不获利，则国家每月至少需要补贴多少元才能使该项目不亏损？

（2）该项目每月处理量为多少吨时，才能使每吨的平均处理成本最低？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】天气预报说，未来三天每天下雨的概率都是0.6，用1、2、3、4表示不下雨，用5、6、7、8、9、0表示下雨，利用计算机生成下列20组随机数，则未来三天恰有两天下雨的概率大约是．
757 220 582 092 103 000 181 249 414 993
010 732 680 596 761 835 463 521 186 289．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】解答题
（1）在边长为1的正方形ABCD内任取一点M，求事件“|AM|≤1”的概率；
（2）某班在一次数学活动中，老师让全班56名同学每人随机写下一对都小于1的正实数x、y，统计出两数能与1构成锐角三角形的三边长的数对（x，y）共有12对，请据此估计π的近似值（精确到0.001）．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】（本小题满分为16分）已知函数．