
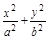 ="1" (a>b>0)的左、右焦点分别为F1、F2, F2也是抛物线C2:y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|=
="1" (a>b>0)的左、右焦点分别为F1、F2, F2也是抛物线C2:y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|=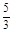 .
.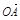 ·
·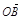 =0,求直线l的方程.
=0,求直线l的方程.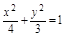 .(2)直线l的方程为y=
.(2)直线l的方程为y=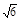 x-2
x-2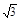 ,或y=
,或y=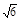 x+2
x+2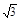 .
.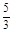 ,所以x1+1=
,所以x1+1=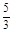 ,得x1=
,得x1=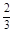 ,y1=
,y1=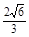 .所以M
.所以M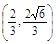 .M在C1上,且椭圆C1的半焦距c=1,于是
.M在C1上,且椭圆C1的半焦距c=1,于是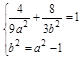 消去b2并整理得9a4-37a2+4=0.
消去b2并整理得9a4-37a2+4=0.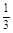 不合题意,舍去). b2=4-1=3.故椭圆C1的方程为
不合题意,舍去). b2=4-1=3.故椭圆C1的方程为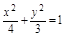 .
. =
=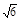 .设l的方程为y=
.设l的方程为y=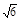 (x-m).
(x-m). 消去y并整理得9x2-16mx+8m2-4=0.设A(x1,y1),B(x2,y2),则x1+x2=
消去y并整理得9x2-16mx+8m2-4=0.设A(x1,y1),B(x2,y2),则x1+x2=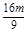 ,x1x2=
,x1x2=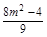 .
.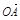 ⊥
⊥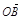 ,所以x1x2+y1y2=0.所以x1x2+y1y2=x1x2+6(x1-m)(x2-m)=7x1x2-6m(x1+x2)+6m2
,所以x1x2+y1y2=0.所以x1x2+y1y2=x1x2+6(x1-m)(x2-m)=7x1x2-6m(x1+x2)+6m2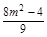 -6m·
-6m·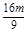 +6m2=
+6m2=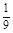 (14m2-28)=0.所以m=±
(14m2-28)=0.所以m=± .此时Δ=(16m)2-4×9(8m2-4)>0.
.此时Δ=(16m)2-4×9(8m2-4)>0.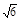 x-2
x-2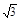 ,或y=
,或y=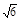 x+2
x+2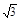 .
.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源:不详 题型:解答题
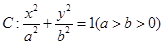 的离心率为
的离心率为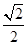 ,
,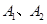 是椭圆的左右顶点,
是椭圆的左右顶点,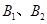 是椭圆的上下顶点,四边形
是椭圆的上下顶点,四边形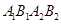 的面积为
的面积为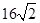 .
.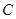 的方程;
的方程;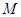 过
过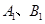 两点.当圆心
两点.当圆心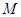 与原点
与原点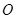 的距离最小时,求圆
的距离最小时,求圆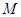 的方程.
的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.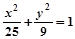 (y≠0) (y≠0) | B.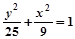 (y≠0) (y≠0) |
C.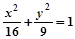 (y≠0) (y≠0) | D.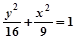 (y≠0) (y≠0) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
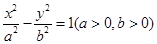 与椭圆
与椭圆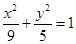 有相同的焦点
有相同的焦点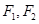 ,且该双曲线
,且该双曲线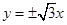 .
.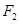 作斜率不为零的直线与此双曲线的左,右两支分别交于点
作斜率不为零的直线与此双曲线的左,右两支分别交于点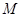 、
、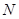 ,
,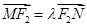 ,当
,当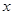 轴上的点
轴上的点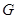 满足
满足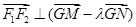 时,求点
时,求点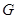 的坐标.
的坐标.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 O
O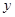 中,直线
中,直线 与抛物线
与抛物线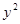 =2
=2 相交于A、B两点。
相交于A、B两点。 过点T(3,0),那么
过点T(3,0),那么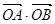 =3”是真命题;
=3”是真命题;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com