Question

9．函数y=2sinπx（x∈R）的部分图象如图所示，设O为坐标原点，P是图象的最高点，B是图象与x轴的交点，则tan∠OPB的值为$\frac{16}{3}$．

Answer 1

分析 过P作PQ垂直于x轴，根据正弦函数的图象与性质，得出点P、B和Q的坐标，计算|PQ|，|OQ|，|BQ|的长，
利用锐角三角函数定义表示出tan∠OPQ和tan∠BPQ，计算tan∠OPB的值即可．

解答 解：过P作PQ⊥x轴，如图所示：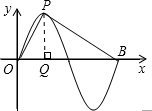

∵函数y=2sinπx，且P是图象的最高点，B是图象与x轴的交点，
∴P（$\frac{1}{2}$，2），B（2，0），
即|PQ|=2，|OQ|=$\frac{1}{2}$，|OB|=2，
∴|QB|=|OB|-|OQ|=$\frac{3}{2}$，
在Rt△OPQ中，tan∠OPQ=$\frac{|OQ|}{|PQ|}$=$\frac{1}{4}$，
在Rt△PQB中，tan∠BPQ=$\frac{|BQ|}{|PQ|}$=$\frac{3}{4}$，
∴tan∠OPB=tan（∠OPQ+∠BPQ）=$\frac{\frac{1}{4}+\frac{3}{4}}{1-\frac{1}{4}×\frac{3}{4}}$=$\frac{16}{3}$．
故答案为：$\frac{16}{3}$．

点评 本题考查了两角和与差的正切函数公式，锐角三角函数定义以及正弦函数的图象与性质，作出辅助线PQ，找P、B的坐标是解题的关键．