
 和直线
和直线 .
. 取何值,直线
取何值,直线 和圆
和圆 总相交;
总相交; 取何值时,圆
取何值时,圆 被直线
被直线 截得的弦长最短?并求最短的弦的长度.
截得的弦长最短?并求最短的弦的长度. 的方程可化为:
的方程可化为: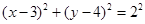 ,圆心为
,圆心为 ,半径
,半径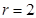 .
. 的方程可化为:
的方程可化为: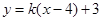 ,直线过定点
,直线过定点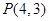 ,斜率为
,斜率为 .
.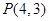 到圆心
到圆心 的距离
的距离 ,
,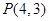 在圆
在圆 内部,∴不论
内部,∴不论 取何值,直线
取何值,直线 和圆
和圆 总相交.
总相交. 的方程可化为:
的方程可化为: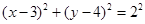 ,圆心为
,圆心为 ,半径
,半径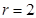 .
. 到直线
到直线 的距离
的距离 ,
,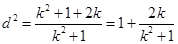 ,因
,因 ,
,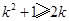 ,
, ,
, ,∴不论
,∴不论 取何值,直线
取何值,直线 和圆
和圆 总相交.
总相交. 到直线
到直线 的距离
的距离
 被直线
被直线 截得的弦长=
截得的弦长=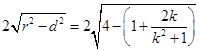 ,
, 时,弦长
时,弦长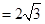 ;
;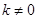 时,弦长
时,弦长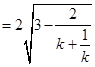 ,下面考虑先求函数
,下面考虑先求函数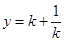 的值域.
的值域.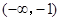 上单调递增,在
上单调递增,在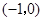 上单调递减,在
上单调递减,在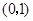 上单调递减,在
上单调递减,在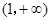 上单调递增(证明略),
上单调递增(证明略),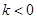 时,函数在
时,函数在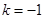 处取得最大值-2;当
处取得最大值-2;当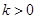 时,函数在
时,函数在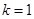 处取得最小值2.
处取得最小值2.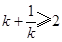 或
或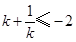 ,
,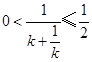 或
或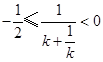 ,可得
,可得 或
或 ,即
,即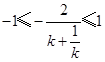 且
且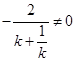 ,
, 且
且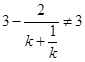 ,
,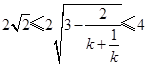 且
且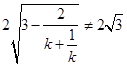 .
.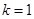 时,弦长取得最小值
时,弦长取得最小值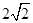 ;当
;当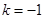 时,弦长取得最大值4.
时,弦长取得最大值4.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| α |
| β |
| α |
| β |
| β |
| α |
| α |
| β |
| α |
| β |
| β |
| β |
| α |
| β |
| β |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,相应于焦点F(c,0)(c>0)的准线
,相应于焦点F(c,0)(c>0)的准线 与x轴交于点A,且|OF|=3|OA|,过点F的直线与双曲线交于P、Q两点.
与x轴交于点A,且|OF|=3|OA|,过点F的直线与双曲线交于P、Q两点. =0,求直线PQ的方程.
=0,求直线PQ的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 程为________.
程为________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com