
 ,相应于焦点F(c,0)(c>0)的准线
,相应于焦点F(c,0)(c>0)的准线 与x轴交于点A,且|OF|=3|OA|,过点F的直线与双曲线交于P、Q两点.
与x轴交于点A,且|OF|=3|OA|,过点F的直线与双曲线交于P、Q两点. =0,求直线PQ的方程.
=0,求直线PQ的方程. = 1
= 1 -3 = 0或x +
-3 = 0或x + -3 = 0
-3 = 0 = 1(a>0,b>0)
= 1(a>0,b>0) 解得a =
解得a = ,c = 3所以双曲线的方程为
,c = 3所以双曲线的方程为 = 1…(6分)
= 1…(6分) ≠0,应舍去.
≠0,应舍去. 得
得 
 -2≠0,即k≠
-2≠0,即k≠ ,
, -4(
-4( -2)(9
-2)(9 +6)=48(
+6)=48( +1)>0即k∈R.
+1)>0即k∈R. (*) ………………………(8分)
(*) ………………………(8分) ,
, ),Q(
),Q( ,
, ),则
),则
 = k(
= k( -3),
-3), = k(
= k( -3)
-3)
 =
= (
( -3)(
-3)( -3)=
-3)= [
[
 -3(
-3( +
+ )+ 9] (3)
)+ 9] (3) = 0,∴(
= 0,∴( -1,
-1, )·(
)·( -1,
-1, )= 0
)= 0
 -(
-( +
+ )+ 1 +
)+ 1 + 
 =" 0 " (4)
=" 0 " (4) = 0
= 0 =
= ,∴k =
,∴k = 满足(*)
满足(*) -3 = 0或x +
-3 = 0或x + -3 = 0………(13分)
-3 = 0………(13分)

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源:不详 题型:解答题
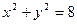 上的点的横坐标保持不变,纵坐标变为原来的
上的点的横坐标保持不变,纵坐标变为原来的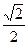 倍,得到曲线
倍,得到曲线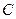 .设直线
.设直线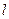 与曲线
与曲线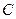 相交于
相交于 、
、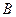 两点,且
两点,且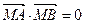 ,其中
,其中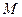 是曲线
是曲线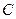 与
与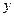 轴正半轴的交点.
轴正半轴的交点.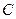 的方程;
的方程;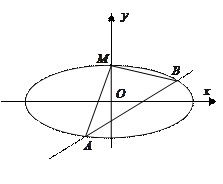 (Ⅱ)证明:直线
(Ⅱ)证明:直线 的纵截距为定值.
的纵截距为定值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
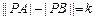 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;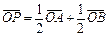 ,则动点P的轨迹为椭圆;
,则动点P的轨迹为椭圆;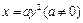 的焦点坐标是
的焦点坐标是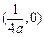 ;
;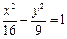 与曲线
与曲线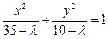 (
(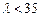 且
且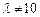 )有相同的焦点.
)有相同的焦点.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
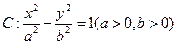 的离心率为
的离心率为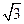 ,右准线为
,右准线为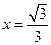 。
。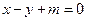 与双曲线C交于不同的两点A,B,且线段AB的中点在圆
与双曲线C交于不同的两点A,B,且线段AB的中点在圆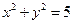 上,求m的值.
上,求m的值. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com