
 经过点
经过点 ,对称轴为坐标轴,焦点
,对称轴为坐标轴,焦点 在
在 轴上,离心率
轴上,离心率 .
. 的方程;
的方程; 的角平分线所在直线
的角平分线所在直线 的方程;
的方程; 上是否存在关于直线
上是否存在关于直线 对称的相异两点?
对称的相异两点?
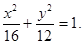 (2)
(2)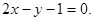 (3)不存在满足题设条件的点B和C.
(3)不存在满足题设条件的点B和C.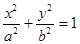 ,
,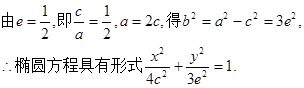
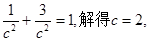
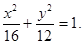
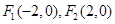 ,所以直线AF1的方程为:
,所以直线AF1的方程为: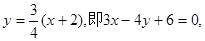 直线AF2的方程为:
直线AF2的方程为: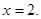 由点A在椭圆E上的位置知,直线l的斜率为正数.设
由点A在椭圆E上的位置知,直线l的斜率为正数.设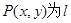 上任一点,则
上任一点,则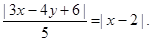 若
若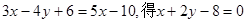 (因其斜率为负,舍去).
(因其斜率为负,舍去).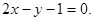
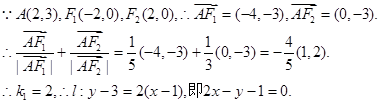
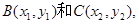
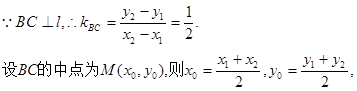
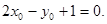 ①
①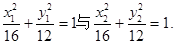 两式相减,得
两式相减,得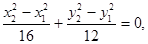
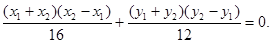 将该式写为
将该式写为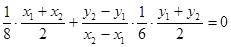 ,并将直线BC的斜率
,并将直线BC的斜率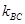 和线段BC的中点,表示代入该表达式中,得
和线段BC的中点,表示代入该表达式中,得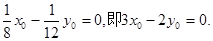 ②
②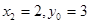 ,即BC的中点为点A,而这是不可能的.
,即BC的中点为点A,而这是不可能的.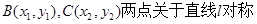 ,则
,则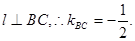
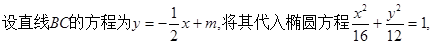 得一元二次方程
得一元二次方程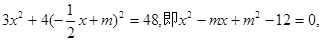 则
则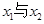 是该方程的两个根,由韦达定理得
是该方程的两个根,由韦达定理得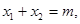 于是
于是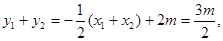 ∴B,C的中点坐标为
∴B,C的中点坐标为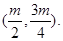 又线段BC的中点在直线
又线段BC的中点在直线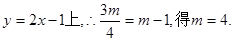


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com