
已知函数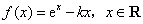 .
.
(1)若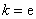 ,试确定函数
,试确定函数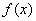 的单调区间;
的单调区间;
(2)若 ,且对于任意
,且对于任意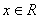 ,
,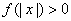 恒成立,试确定实数
恒成立,试确定实数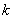 的取值范围;
的取值范围;
(3)设函数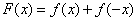 ,求证:
,求证: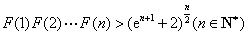 .
.
科目:高中数学 来源: 题型:
如图,椭圆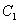 :
: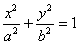 (
(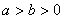 )和圆
)和圆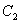 :
: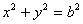 ,已知圆
,已知圆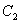 将椭圆
将椭圆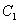 的长轴三等分,且
的长轴三等分,且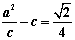 ,椭圆
,椭圆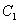 的下顶点为
的下顶点为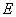 ,过坐标原点
,过坐标原点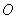 且与坐标轴不重合的任意直线
且与坐标轴不重合的任意直线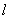 与圆
与圆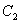 相交于点
相交于点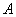 、
、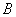 .
.
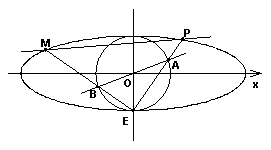 (Ⅰ )求椭圆
(Ⅰ )求椭圆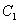 的方程;
的方程;
(Ⅱ )若直线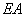 、
、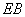 分别与椭圆
分别与椭圆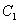 相交于另一个交点为点
相交于另一个交点为点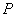 、
、 .
.
① 求证:直线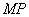 经过一定点;
经过一定点;
② 试问:是否存在以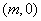 为圆心,
为圆心,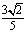 为半径的圆
为半径的圆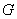 ,使得直线
,使得直线 和直线
和直线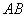 都与圆
都与圆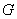 相交?若存在,请求出所有
相交?若存在,请求出所有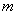 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
六人按下列要求站一横排,分别有多少种不同的站法?
(l)甲不站两端;
(2)甲、乙不相邻;
(3)甲、乙之间间隔两人;
(4)甲不站左端,乙不站右端.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题中
①若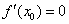 ,则函数
,则函数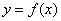 在
在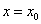 取得极值;
取得极值;
②直线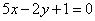 与函数
与函数 的图像不相切;
的图像不相切;
③若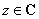 (
(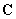 为复数集),且
为复数集),且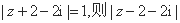 的最小值是
的最小值是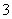 ;
;
④定积分 .
.
正确的有.
A.①④ B.③④ C.②④ D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
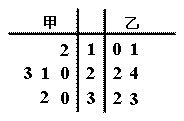 2015赛季CBA(中国男子职业篮球联赛)总决赛于3月22号结束,北京首钢队4∶2战胜辽宁药都队卫冕成功。如图是参加此次总决赛的甲、乙两名运动员在6场比赛中的得分茎叶图,两人得分的平均数分别为
2015赛季CBA(中国男子职业篮球联赛)总决赛于3月22号结束,北京首钢队4∶2战胜辽宁药都队卫冕成功。如图是参加此次总决赛的甲、乙两名运动员在6场比赛中的得分茎叶图,两人得分的平均数分别为 、
、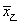 ,得分的标准差分别为
,得分的标准差分别为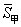 、
、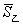 ,则下面正确的结论是( )
,则下面正确的结论是( )
A.
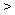
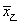 ,
,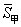
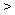
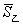 B.
B.
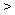
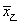 ,
,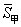
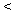
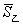
C.
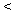
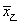 ,
,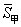
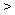
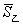 D.
D.
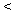
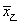 ,
,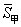
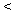
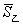
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com