
如图,椭圆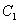 :
: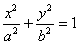 (
(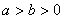 )和圆
)和圆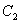 :
: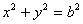 ,已知圆
,已知圆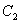 将椭圆
将椭圆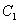 的长轴三等分,且
的长轴三等分,且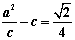 ,椭圆
,椭圆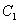 的下顶点为
的下顶点为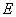 ,过坐标原点
,过坐标原点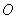 且与坐标轴不重合的任意直线
且与坐标轴不重合的任意直线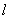 与圆
与圆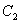 相交于点
相交于点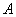 、
、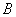 .
.
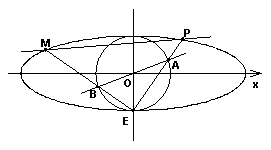 (Ⅰ )求椭圆
(Ⅰ )求椭圆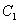 的方程;
的方程;
(Ⅱ )若直线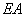 、
、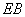 分别与椭圆
分别与椭圆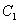 相交于另一个交点为点
相交于另一个交点为点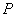 、
、 .
.
① 求证:直线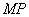 经过一定点;
经过一定点;
② 试问:是否存在以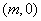 为圆心,
为圆心,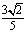 为半径的圆
为半径的圆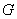 ,使得直线
,使得直线 和直线
和直线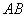 都与圆
都与圆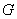 相交?若存在,请求出所有
相交?若存在,请求出所有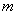 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅰ )依题意, ,则
,则 ,
,
∴ ,又
,又 ,∴
,∴ ,则
,则 ,
,
∴椭圆方程为 .————————3分
.————————3分
(Ⅱ)①由题意知直线 的斜率存在且不为0,设直线
的斜率存在且不为0,设直线 的斜率为
的斜率为 ,则
,则 :
: ,
,
由 得
得 或
或
∴ ,————————5分
,————————5分
用 去代
去代 ,得
,得 ,
,
方法1: ,
,
∴ :
: ,即
,即 ,——6分
,——6分
∴直线 经过定点
经过定点 .——————7分
.——————7分
方法2:作直线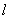 关于
关于 轴的对称直线
轴的对称直线 ,此时得到的点
,此时得到的点 、
、 关于
关于 轴对称,则
轴对称,则 与
与 相交于
相交于 轴,可知定点在
轴,可知定点在 轴上,
轴上,
当 时,
时, ,
, ,此时直线
,此时直线 经过
经过 轴上的点
轴上的点 ,
,
∵

∴ ,∴
,∴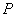 、
、 、
、 三点共线,即直线
三点共线,即直线 经过点
经过点 ,
,
综上所述,直线 经过定点
经过定点 .
.
②由 得
得 或
或 ∴
∴ ,
,
则直线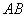 :
: ,
,
设 ,则
,则 ,直线
,直线 :
: ,直线
,直线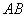 :
: ,
,
假设存在圆心为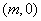 ,半径为
,半径为 的圆
的圆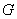 ,使得直线
,使得直线 和直线
和直线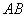 都与圆
都与圆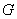 相交,
相交,
则 由(
由( )得
)得 对
对 恒成立,则
恒成立,则 ,
,
由( )得,
)得, 对
对 恒成立,
恒成立,
当 时,不合题意;当
时,不合题意;当 时,
时, ,得
,得 ,即
,即 ,
,
∴存在圆心为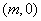 ,半径为
,半径为 的圆
的圆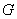 ,使得直线
,使得直线 和直线
和直线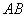 都与圆
都与圆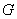 相交,所有
相交,所有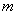 的取值集合为
的取值集合为 .
.
解法二:圆 ,由上知
,由上知 过定点
过定点 ,故
,故 ;又直线
;又直线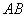 过原点,故
过原点,故 ,从而得
,从而得 .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
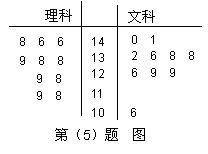
某校在一次期中考试结束后,把全校文、理科总分前10名学生的数学成绩(满分150分)抽出来进行对比分析,得到如图所示的茎叶图.若从数学成绩高于120分的学生中抽取3人,分别到三个班级进行数学学习方法交流,则满足理科人数多于文科人数的情况有( )种
A. 3081 B. 1512
C. 1848 D. 2014
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com