
【题目】设函数 ![]() .
.
(1)求 ![]() 极值;
极值;
(2)当 ![]() 时,
时, ![]() ,求a的取值范围.
,求a的取值范围.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为U=(0,+![]() ),且满足条件f(4)=1。对任意的x1,x2∈U,有f(x1·x2)=f(x1)+f(x2),且当x1≠x2时,有
),且满足条件f(4)=1。对任意的x1,x2∈U,有f(x1·x2)=f(x1)+f(x2),且当x1≠x2时,有![]() >0。
>0。
(1)求f(1)的值;
(2)如果f(x+6)+f(x)>2,求x的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ax2+2(a﹣3)x+1在区间[﹣2,+∞)上递减,则实数a的取值范围是( )
A.(﹣∞,0)
B.[﹣3,+∞)
C.[﹣3,0]
D.(0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该市决定在第3,4组的志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率. 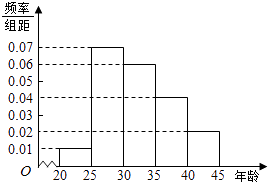
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 ![]() 中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线
中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线 ![]() 的极坐标方程是
的极坐标方程是 ![]() ,圆
,圆 ![]() 的极坐标方程是
的极坐标方程是 ![]() .
.
(1)求 ![]() 与
与 ![]() 交点的极坐标;
交点的极坐标;
(2)设 ![]() 为
为 ![]() 的圆心,
的圆心, ![]() 为
为 ![]() 与
与 ![]() 交点连线的中点,已知直线
交点连线的中点,已知直线 ![]() 的参数方程是
的参数方程是 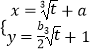 (
( ![]() 为参数),求
为参数),求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知α,β是平面,m,n是直线.下列命题中不正确的是 ( )
A.若m∥n,m⊥α,则n⊥α
B.若m∥α,α∩β=n,则m∥n
C.若m⊥α,m⊥β,则α∥β
D.若m⊥α, ![]() ,则α⊥β
,则α⊥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ,
,![]() 为常量,且
为常量,且![]() ,
,![]() 的图象经过点
的图象经过点![]() ,
,![]() .
.
(![]() )求
)求![]() ,
,![]() 的值.
的值.
(![]() )当
)当![]() 时,函数
时,函数![]() 的图像恒在函数
的图像恒在函数![]() 图像的上方,求实数
图像的上方,求实数![]() 的取值范围.
的取值范围.
(![]() )定义在
)定义在![]() 上的一个函数
上的一个函数![]() ,如果存在一个常数
,如果存在一个常数![]() ,使得式子
,使得式子![]() 对一切大于
对一切大于![]() 的自然数
的自然数![]() 都成立,则称函数
都成立,则称函数![]() 为“
为“![]() 上的
上的![]() 函数”(其中,
函数”(其中,![]() .试判断函数
.试判断函数![]() 是否为“
是否为“![]() 上的
上的![]() 函数”.若是,则求出
函数”.若是,则求出![]() 的最小值;若不是,则请说明理由.(注:
的最小值;若不是,则请说明理由.(注:![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com