
已知函数f(x)是定义在R上的奇函数,若对于任意给定的不等实数x1,x2不等式x1f(x1)+x2f(x2)<x1f(x2)+x2f(x1)恒成立,则不等式f(1-x)<0的解集为( )
A.(-∞,0) B.(0,+∞)
C.(-∞,1) D.(1,+∞)
 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=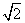 ,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
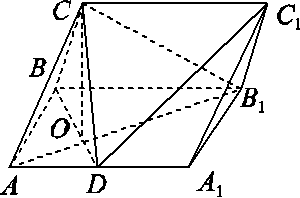
(1)证明:BC⊥AB1;
(2)若OC=OA,求三棱锥C1-ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(x)=2x2+px+q,g(x)=x+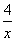 是定义在集合M=
是定义在集合M=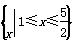 上的两个函数.对任意的x∈M,存在常数x0∈M,使得f(x)≥f(x0),g(x)≥g(x0),且f(x0)=g(x0).则函数f(x)在集合M上的最大值为( )
上的两个函数.对任意的x∈M,存在常数x0∈M,使得f(x)≥f(x0),g(x)≥g(x0),且f(x0)=g(x0).则函数f(x)在集合M上的最大值为( )
A. B.4
B.4
C.6 D.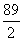
查看答案和解析>>
科目:高中数学 来源: 题型:
若函数f(x),g(x)分别为R上的奇函数和偶函数,且满足f(x)-g(x)=ex,则有( )
A.f(2)<f(3)<g(0) B.g(0)<f(3)<f(2)
C.f(2)<g(0)<f(3) D.g(0)<f(2)<f(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙、丙3位教师安排在周一至周五中的3天值班,要求每人值班1天且每天至多安排1人,则恰好甲安排在另外两位教师前面值班的概率是( )
A.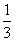 B.
B.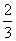 C.
C.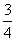 D.
D.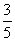
查看答案和解析>>
科目:高中数学 来源: 题型:
节能灯的质量通过其正常使用时间来衡量,使用时间越长,表明质量越好,且使用时间大于或等于6千小时的产品为优质品.现用A,B两种不同型号的节能灯做试验,各随机抽取部分产品作为样本,得到试验结果的频率分布直方图如图所示.

以上述试验结果中使用时间落入各组的频率作为相应的概率.
(1)现从大量的A,B两种型号节能灯中各随机抽取两件产品,求恰有两件是优质品的概率;
(2)已知A型节能灯的生产厂家对使用时间小于6千小时的节能灯实行“三包”.通过多年统计发现,A型节能灯每件产品的利润y(单位:元)与其使用时间t(单位:千小时)的关系如下表:
| 使用时间t (单位:千小时) | t<4 | 4≤t<6 | t≥6 |
| 每件产品的 利润y(单位:元) | -20 | 20 | 40 |
若从大量的A型节能灯中随机抽取两件,其利润之和记为X(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
命题p为:抛物线x2=4y的焦点坐标为(0,1);命题q为:“a=3”是“直线ax+2y=0与直线2x-3y=3垂直”的充要条件.则以下结论正确的是( )
A.p或q为真命题 B.p且q为假命题
C.p且綈q为真命题 D.綈p或q为假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com