
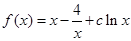 ,其中
,其中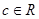 ,
,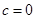 时,求曲线
时,求曲线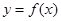 在点
在点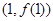 处的切线方程;
处的切线方程;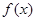 的单调性;
的单调性;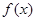 有两个极值点
有两个极值点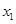 和
和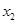 ,记过点
,记过点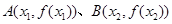 的直线的斜率为
的直线的斜率为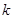 ,问是否存在
,问是否存在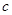 ,使得
,使得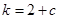 ?若存在,求出
?若存在,求出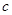 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.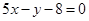 ;(2)
;(2)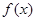 分别在
分别在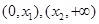 上单调递增,在
上单调递增,在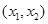 上单调递减;(3)不存在
上单调递减;(3)不存在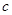 ,使得
,使得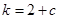 .
.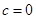 时,
时,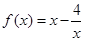 ,那么曲线
,那么曲线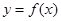 在点
在点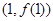 处的切线的斜率
处的切线的斜率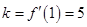 ,根据点斜式写出直线的方程为
,根据点斜式写出直线的方程为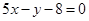 ;(2)函数
;(2)函数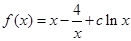 求导得
求导得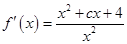 ,
,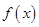 的定义域是
的定义域是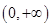 ,因此只需要讨论分子在
,因此只需要讨论分子在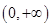 上的正负问题;(3)假设存在
上的正负问题;(3)假设存在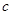 ,使得
,使得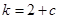 ,那么计算出
,那么计算出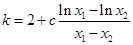 ,问题归结为
,问题归结为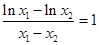 是否成立,可设函数
是否成立,可设函数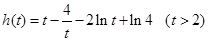 ,
,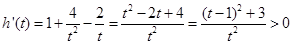 ,所以
,所以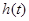 在
在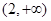 上单调递增,因此不存在
上单调递增,因此不存在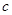 ,使得
,使得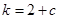 .
.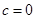 时,
时,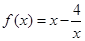 ,所以
,所以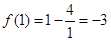
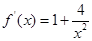 ,
, 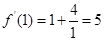 ,
, 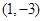 ,所以切线方程为
,所以切线方程为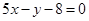
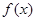 的定义域为
的定义域为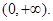
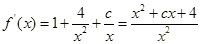 ,
,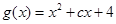 ,其判别式
,其判别式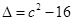
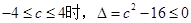 ,故
,故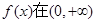 上单调递增
上单调递增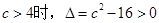 ,
,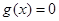 的两根都小于0,在
的两根都小于0,在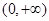 上,
上,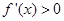 ,故
,故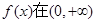 上单调递增.
上单调递增. 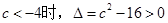 ,设
,设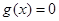 的两根为,
的两根为,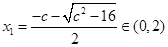
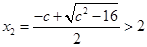
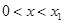 时,
时, 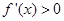 ;当
;当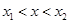 时,
时, 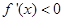 ;当
;当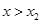 时,
时, 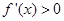 ,故
,故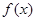 分别在
分别在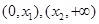 上单调递增,在
上单调递增,在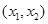 上单调递减.
上单调递减. 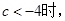
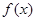 在
在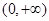 上有两个极值点
上有两个极值点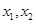
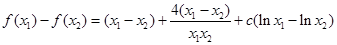
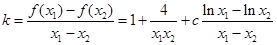
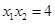 ,于是
,于是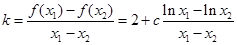 ,
,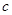 ,使得
,使得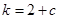 ,则
,则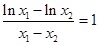 ,即
,即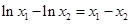 ,
,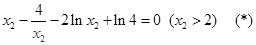
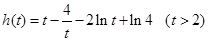 ,
,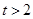 时,
时,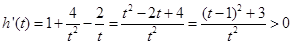 ,所以
,所以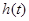 在
在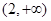 上单调递增,
上单调递增, 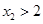 ,所以
,所以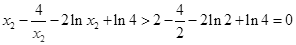 ,
,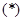 式矛盾.故不存在
式矛盾.故不存在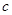 ,使得
,使得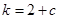


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
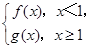 若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
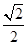 ,
,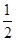 ),则函数g(x)=
),则函数g(x)=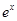 f(x)的单调递减区间为( )
f(x)的单调递减区间为( )| A.(-∞,0) | B.(-∞,-2) | C.(-2,-1) | D.(-2,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com