解:(Ⅰ)证明:f'(x)=-e
-x(cosx+sinx)+e
-x(-sinx+cosx)=-2e
-xsinx.
由f'(x)=0,得-2e
-xsinx=0.
解出x=nπ,n为整数,从而x
n=nπ,n=1,2,3,f(x
n)=(-1)
ne
-nπ.
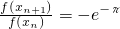
.
所以数列{f{x
n}}是公比q=-e
-π的等比数列,且首项f(x
1)=q.
(Ⅱ)解:S
n=x
1f(x
1)+x
2f(x
2)++x
nf(x
n)=πq(1+2q++nq
n-1),
qS
n=πq(q+2q
2++nq
n),
S
n-qS
n=πq(1+2q
2++q
n-1-nq
n)
=
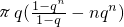
,
从而
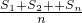
=
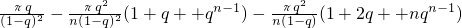
=
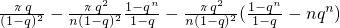
=
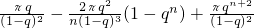
.
因为
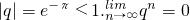
,
所以
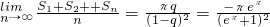
.
分析:(1)先求导数,解出f'(x)=0的所有正数解x,求得数列{x
n}.从而可证明数列{f{x
n}}为等比数列.
(2)利用错位相减法求得Sn,从而求得
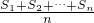
,进而得解.
点评:本小题主要考查.函数求导,等比数列证明,错位相减的求和方法,及极限的求解等知识.是对知识的综合性考查,能力要求较高.

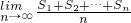 .
.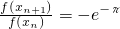 .
.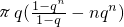 ,
,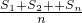
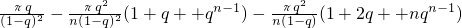
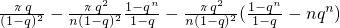
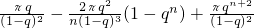 .
.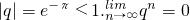 ,
,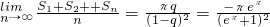 .
.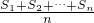 ,进而得解.
,进而得解.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案