【题目】已知F是抛物线y2=4x的焦点，点A，B在该抛物线上且位于x轴的两侧，OA⊥OB（其中O为坐标原点），则△AOB与△AOF面积之和的最小值是（ ）
A.16
B.8
C.8
D.18
【答案】C
【解析】解：设直线AB的方程为：x=ty+m，
点A（x1 ， y1），B（x2 ， y2），直线AB与x轴的交点为M（m，0），
x=ty+m代入y2=4x，可得y2﹣4ty﹣4m=0，
根据韦达定理有y1y2=﹣4m，
∵OA⊥OB，
∴
=0，
∴x1x2+y1y2=0，从而（
y1y2）2+y1y2=0，
∵点A，B位于x轴的两侧，
∴y1y2=﹣16，故m=4．
不妨令点A在x轴上方，则y1＞0，
又F（1，0），
∴S△ABO+S△AFO=
×4×（y1﹣y2）+×y1=
y1+
≥8
，
当且仅当y1= ， 即y1=
时，取“=”号，
∴△ABO与△AFO面积之和的最小值是8 ，
故选：C．
科目：高中数学 来源： 题型：
【题目】如图，在正方体ABCDA1B1C1D1中，O为底面ABCD的中心，P,Q分别为
的中点．
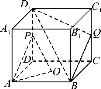
求证：(1)平面D1 BQ∥平面PAO.
(2)求异面直线QD1与AO所成角的余弦值；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若
则一定有（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】本题主要考查不等关系。已知
,所以
，所以
，故
。故选
【题型】单选题
【结束】
5
【题目】关于x的不等式ax2＋bx＋2>0的解集为{x|－1<x<2}，则关于x的不等式bx2－ax－2>0的解集为( )
A. {x|－2<x<1} B. {x|x>1或x<－2}
C. {x|x>2或x<－1} D. {x|x<－1或x>1}
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设B、C是定点，且均不在平面α上，动点A在平面α上，且sin∠ABC=
， 则点A的轨迹为（ ）
A.圆或椭圆
B.抛物线或双曲线
C.椭圆或双曲线
D.以上均有可能
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知等比数列{an}、等差数列{bn}，满足a1＞0，b1=a1﹣1，b2=a2 ， b3=a3且数列{an}唯一．
（1）求数列{an}，{bn}的通项公式；
（2）求数列{anbn}的前n项和．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}满足a1=1，an+1=2an+1．
（1）求数列{an}的通项公式；
（2）令bn=
n（an+1），求数列{bn}的前n项和Tn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知A(1,0,0)，B(0,1,0)，C(0,0,2)．
(1)若
∥
，
∥
，求点D的坐标；
(2)问是否存在实数α，β，使得＝α＋β
成立？若存在，求出α，β的值；若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分12分）
如图1，在Rt
中，
，
.D、E分别是
上的点，且
，将
沿
折起到
的位置，使
，如图2．
（Ⅰ）求证：平面
平面
；
（Ⅱ）若
，求
与平面
所成角的余弦值；
（Ⅲ）当
点在何处时，
的长度最小，并求出最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义在R上的奇函数f（x）满足f（x+1）=f（﹣x），当x∈（0，1）时，f（x）=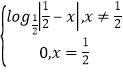
， 则f（x）在区间（1，
）内是（ ）
A.增函数且f（x）＞0
B.增函数且f（x）＜0
C.减函数且f（x）＞0
D.减函数且f（x）＜0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com