
 ,设该椭圆上的点到左焦点F(-c,0)的最大距离为d1,到右顶点A(a,0)的最大距离为d2.
,设该椭圆上的点到左焦点F(-c,0)的最大距离为d1,到右顶点A(a,0)的最大距离为d2. .
.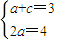
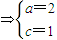 ,由此能求出椭圆E的方程.
,由此能求出椭圆E的方程.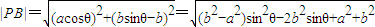 ,先构造二次函数f(t)=-c2t2-2b2t+a2+b2(-1≤t≤1),再由分类讨论思想能求出椭圆上的点到上顶点的最大距离.
,先构造二次函数f(t)=-c2t2-2b2t+a2+b2(-1≤t≤1),再由分类讨论思想能求出椭圆上的点到上顶点的最大距离.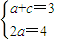
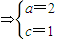 ,
,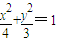 ;…(5分)
;…(5分)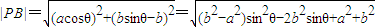 ,
,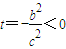 .
. ,
,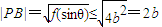 ,
,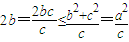 ,从而
,从而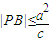 ;
;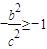 ,即b2≤c2时,
,即b2≤c2时,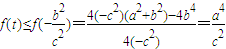 ,
, ;
;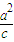 ,
,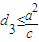 .…(15分)
.…(15分)

科目:高中数学 来源:浙江省宁波市鄞州区2012届高三高考适应性考试(3月)数学理科试题 题型:044
已知椭圆E:![]() ,设该椭圆上的点到左焦点F(-c,0)的最大距离为d1,到右顶点A(a,0)的最大距离为d2.
,设该椭圆上的点到左焦点F(-c,0)的最大距离为d1,到右顶点A(a,0)的最大距离为d2.
(Ⅰ)若d1=3,d2=4,求椭圆E的方程;
(Ⅱ)设该椭圆上的点到上顶点B(0,b)的最大距离为d3,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省宁波市鄞州区高三高考适应性3月考试理科数学 题型:解答题
(本小题满分15分)已知椭圆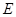 :
: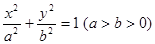 ,设该椭圆上的点到左焦点
,设该椭圆上的点到左焦点
 的最大距离为
的最大距离为 ,到右顶点
,到右顶点
 的最大距离为
的最大距离为 .
.
(Ⅰ)
若 ,
, ,求椭圆
,求椭圆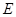 的方程;
的方程;
(Ⅱ)
设该椭圆上的点到上顶点
 的最大距离为
的最大距离为 ,求证:
,求证: .
.
查看答案和解析>>
科目:高中数学 来源:浙江省模拟题 题型:解答题
 ,设该椭圆上的点到左焦点F(-c,0)的最大距离为d1,到右顶点A(a,0)的最大距离为d2,
,设该椭圆上的点到左焦点F(-c,0)的最大距离为d1,到右顶点A(a,0)的最大距离为d2, 。
。查看答案和解析>>
科目:高中数学 来源:浙江省宁波市鄞州区2011-2012学年高三高考适应性考试(3月)数学(理)试题 题型:解答题
已知椭圆 :
: ,设该椭圆上的点到左焦点
,设该椭圆上的点到左焦点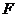
 的最大距离为
的最大距离为 ,到右顶点
,到右顶点
 的最大距离为
的最大距离为 .
.
(Ⅰ) 若 ,
, ,求椭圆
,求椭圆 的方程;
的方程;
(Ⅱ) 设该椭圆上的点到上顶点
 的最大距离为
的最大距离为 ,求证:
,求证: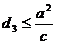 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com