
【题目】已知数列![]() 是各项均不为0的等差数列,公差为
是各项均不为0的等差数列,公差为![]() ,
,![]() 为其前
为其前![]() 项和,且满足
项和,且满足![]() .数列
.数列![]() 满足
满足![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1)求![]() ;
;
(2)求![]() ;
;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】某公司举办捐步公益活动,参与者通过捐赠每天的运动步数获得公司提供的牛奶,再将牛奶捐赠给留守儿童.此活动不但为公益事业作出了较大的贡献,公司还获得了相应的广告效益.据测算,首日参与活动人数为![]() 人,以后每天人数比前一天都增加
人,以后每天人数比前一天都增加![]() ,
,![]() 天后捐步人数稳定在第
天后捐步人数稳定在第![]() 天的水平,假设此项活动的启动资金为
天的水平,假设此项活动的启动资金为![]() 万元,每位捐步者每天可以使公司收益
万元,每位捐步者每天可以使公司收益![]() 元(以下人数精确到
元(以下人数精确到![]() 人,收益精确到
人,收益精确到![]() 元).
元).
(1)求活动开始后第![]() 天的捐步人数,及前
天的捐步人数,及前![]() 天公司的捐步总收益;
天公司的捐步总收益;
(2)活动开始第几天以后公司的捐步总收益可以收回启动资金并有盈余?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆
,以原点为圆心,椭圆![]() 的短半轴长为半径的圆与直线
的短半轴长为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆方程;
(Ⅱ)设![]() 为椭圆右顶点,过椭圆
为椭圆右顶点,过椭圆![]() 的右焦点的直线
的右焦点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() ),直线
),直线![]() ,
,![]() 分别交直线
分别交直线![]() 于
于![]() ,
,![]() 两点. 求证:
两点. 求证:![]() ,
,![]() 两点的纵坐标之积为定值.
两点的纵坐标之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
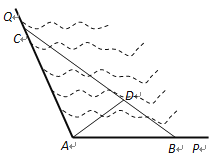
【题目】如图所示,![]() 是某海湾旅游区的一角,其中
是某海湾旅游区的一角,其中![]() ,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸
,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸![]() 和
和![]() 上分别修建观光长廊
上分别修建观光长廊![]() 和AC,其中
和AC,其中![]() 是宽长廊,造价是
是宽长廊,造价是![]() 元/米,
元/米,![]() 是窄长廊,造价是
是窄长廊,造价是![]() 元/米,两段长廊的总造价为120万元,同时在线段
元/米,两段长廊的总造价为120万元,同时在线段![]() 上靠近点
上靠近点![]() 的三等分点
的三等分点![]() 处建一个观光平台,并建水上直线通道
处建一个观光平台,并建水上直线通道![]() (平台大小忽略不计),水上通道的造价是
(平台大小忽略不计),水上通道的造价是![]() 元/米.
元/米.
(1) 若规划在三角形![]() 区域内开发水上游乐项目,要求
区域内开发水上游乐项目,要求![]() 的面积最大,那么
的面积最大,那么![]() 和
和![]() 的长度分别为多少米?
的长度分别为多少米?
(2) 在(1)的条件下,建直线通道![]() 还需要多少钱?
还需要多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() ,
,![]() 是曲线
是曲线![]() 上的任意一点,动点
上的任意一点,动点![]() 满足
满足![]()
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)经过点![]() 的动直线
的动直线![]() 与点
与点![]() 的轨迹方程交于
的轨迹方程交于![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() (异于点
(异于点![]() ),使得
),使得![]() ?若存在,求出
?若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右两个焦点分别为
的左、右两个焦点分别为![]() ,P是椭圆上位于第一象限内的点,
,P是椭圆上位于第一象限内的点,![]() 轴,垂足为Q,
轴,垂足为Q,![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() .
.

(1)求椭圆F的方程:
(2)若M是椭圆上的动点,求![]() 的最大值,并求出
的最大值,并求出![]() 取得最大值时M的坐标.
取得最大值时M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方体![]() 的棱长为2,E、F、G分别为
的棱长为2,E、F、G分别为![]() 的中点,给出下列命题:
的中点,给出下列命题:
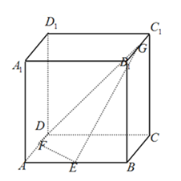
①异面直线EF与AG所成的角的余弦值为![]() ;
;
②过点E、F、G作正方体的截面,所得的截面的面积是![]() ;
;
③![]() 平面
平面![]()
④三棱锥![]() 的体积为1
的体积为1
其中正确的命题是_____________(填写所有正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人们常说的“幸福感指数”就是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间![]() 内的一个数来表示,该数越接近
内的一个数来表示,该数越接近![]() 表示满意度越高.为了解某地区居民的幸福感情况,随机对该地区的男、女居民各
表示满意度越高.为了解某地区居民的幸福感情况,随机对该地区的男、女居民各![]() 人进行了调查,调查数据如表所示:
人进行了调查,调查数据如表所示:
幸福感指数 |
|
|
|
|
|
男居民人数 |
|
|
|
|
|
女居民人数 |
|
|
|
|
|
(1)估算该地区居民幸福感指数的平均值;
(2)若居民幸福感指数不小于![]() ,则认为其幸福.为了进一步了解居民的幸福满意度,调查组又在该地区随机抽取
,则认为其幸福.为了进一步了解居民的幸福满意度,调查组又在该地区随机抽取![]() 对夫妻进行调查,用
对夫妻进行调查,用![]() 表示他们之中幸福夫妻(夫妻二人都感到幸福)的对数,求
表示他们之中幸福夫妻(夫妻二人都感到幸福)的对数,求![]() 的期望(以样本的频率作为总体的概率).
的期望(以样本的频率作为总体的概率).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 点在正方体
点在正方体![]() 的棱
的棱![]() 上(不含端点),给出下列五个命题:
上(不含端点),给出下列五个命题:
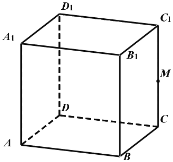
①过![]() 点有且只有一条直线与直线
点有且只有一条直线与直线![]() ,
,![]() 都是异面直线;
都是异面直线;
②过![]() 点有且只有一条直线与直线
点有且只有一条直线与直线![]() ,
,![]() 都相交;
都相交;
③过![]() 点有且只有一条直线与直线
点有且只有一条直线与直线![]() ,
,![]() 都垂直;
都垂直;
④过![]() 点有无数个平面与直线
点有无数个平面与直线![]() ,
,![]() 都相交;
都相交;
⑤过![]() 点有无数个平面与直线
点有无数个平面与直线![]() ,
,![]() 都平行;
都平行;
其中真命题是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com