
【题目】如图所示,![]() 是某海湾旅游区的一角,其中
是某海湾旅游区的一角,其中![]() ,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸
,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸![]() 和
和![]() 上分别修建观光长廊
上分别修建观光长廊![]() 和AC,其中
和AC,其中![]() 是宽长廊,造价是
是宽长廊,造价是![]() 元/米,
元/米,![]() 是窄长廊,造价是
是窄长廊,造价是![]() 元/米,两段长廊的总造价为120万元,同时在线段
元/米,两段长廊的总造价为120万元,同时在线段![]() 上靠近点
上靠近点![]() 的三等分点
的三等分点![]() 处建一个观光平台,并建水上直线通道
处建一个观光平台,并建水上直线通道![]() (平台大小忽略不计),水上通道的造价是
(平台大小忽略不计),水上通道的造价是![]() 元/米.
元/米.
(1) 若规划在三角形![]() 区域内开发水上游乐项目,要求
区域内开发水上游乐项目,要求![]() 的面积最大,那么
的面积最大,那么![]() 和
和![]() 的长度分别为多少米?
的长度分别为多少米?
(2) 在(1)的条件下,建直线通道![]() 还需要多少钱?
还需要多少钱?
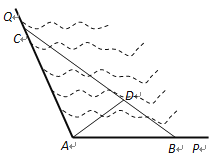
【答案】(1)![]() 和AC的长度分别为750米和1500米(2)
和AC的长度分别为750米和1500米(2)![]() 万元
万元
【解析】
试题(1)设![]() 长为
长为![]() 米,
米,![]() 长为
长为![]() 米,依题意得
米,依题意得![]() ,即
,即![]() ,表示面积,利用基本不等式可得结论;(2)利用向量方法,将
,表示面积,利用基本不等式可得结论;(2)利用向量方法,将![]() 表示为
表示为![]() ,根据向量的数量积与模长的关系可得结果.
,根据向量的数量积与模长的关系可得结果.
试题解析:(1)设![]() 长为
长为![]() 米,
米,![]() 长为
长为![]() 米,依题意得
米,依题意得![]() ,
,
即![]() ,
,
![]()
![]()
![]()
![]() =
=![]()
![]()
当且仅当![]() ,即
,即![]() 时等号成立,
时等号成立,
所以当![]() 的面积最大时,
的面积最大时,![]() 和AC的长度分别为750米和1500米
和AC的长度分别为750米和1500米
(2)在(1)的条件下,因为![]() .
.
由![]()
得![]()
![]()
![]()
![]()
![]() ,
,
![]() 元
元
所以,建水上通道![]() 还需要
还需要![]() 万元.
万元.
解法二:在![]() 中,
中,![]()
![]()
![]()
在![]() 中,
中,![]()
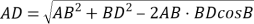
![]()
在![]() 中,
中,![]()
![]() =
=![]()
![]() 元
元
所以,建水上通道![]() 还需要
还需要![]() 万元.
万元.
解法三:以A为原点,以AB为![]() 轴建立平面直角坐标系,则
轴建立平面直角坐标系,则![]() ,
,![]()
![]() ,即
,即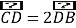 ,设
,设![]()
由![]() ,求得
,求得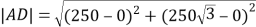 , 所以
, 所以![]()
所以,![]()
![]()
![]() 元
元
所以,建水上通道![]() 还需要
还需要![]() 万元.
万元.


科目:高中数学 来源: 题型:
【题目】垃圾分一分,城市美十分;垃圾分类,人人有责.某市为进一步推进生活垃圾分类工作,调动全民参与的积极性,举办了“垃圾分类游戏挑战赛”.据统计,在为期![]() 个月的活动中,共有
个月的活动中,共有![]() 万人次参与.为鼓励市民积极参与活动,市文明办随机抽取
万人次参与.为鼓励市民积极参与活动,市文明办随机抽取![]() 名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
单次游戏得分 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)根据数据,估计参与活动的网友单次游戏得分的平均值及标准差(同一组中的数据用该组区间的中点值作代表);(其中标准差的计算结果要求精确到![]() )
)
(2)若要从单次游戏得分在![]() 、
、![]() 、
、![]() 的三组参与者中,用分层抽样的方法选取
的三组参与者中,用分层抽样的方法选取![]() 人进行电话回访,再从这
人进行电话回访,再从这![]() 人中任选
人中任选![]() 人赠送话费,求此
人赠送话费,求此![]() 人单次游戏得分不在同一组内的概率.
人单次游戏得分不在同一组内的概率.
附:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为配合“2019双十二”促销活动,某公司的四个商品派送点如图环形分布,并且公司给![]() 四个派送点准备某种商品各50个.根据平台数据中心统计发现,需要将发送给
四个派送点准备某种商品各50个.根据平台数据中心统计发现,需要将发送给![]() 四个派送点的商品数调整为40,45,54,61,但调整只能在相邻派送点进行,每次调动可以调整1件商品.为完成调整,则( )
四个派送点的商品数调整为40,45,54,61,但调整只能在相邻派送点进行,每次调动可以调整1件商品.为完成调整,则( )

A.最少需要16次调动,有2种可行方案
B.最少需要15次调动,有1种可行方案
C.最少需要16次调动,有1种可行方案
D.最少需要15次调动,有2种可行方案
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对城市路网进行改造,拟在原有a个标段(注:一个标段是指一定长度的机动车道)的基础上,新建x个标段和n个道路交叉口,其中n与x满足n=ax+5.已知新建一个标段的造价为m万元,新建一个道路交叉口的造价是新建一个标段的造价的k倍.
(1)写出新建道路交叉口的总造价y(万元)与x的函数关系式;
(2)设P是新建标段的总造价与新建道路交叉口的总造价之比.若新建的标段数是原有标段数的20%,且k≥3.问:P能否大于![]() ,说明理由.
,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰梯形![]() 中,两腰
中,两腰![]() ,底边
,底边![]() 是
是![]() 的三等分点,
的三等分点,![]() 是
是![]() 的中点.分别沿
的中点.分别沿![]() 将四边形
将四边形![]() 和
和![]() 折起,使
折起,使![]() 重合于点
重合于点![]() ,得到如图2所示的几何体.在图2中,
,得到如图2所示的几何体.在图2中,![]() 分别为
分别为![]() 的中点.
的中点.
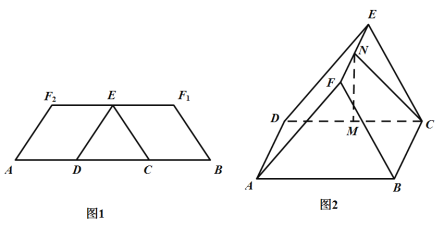
(1)证明:![]() 平面
平面![]()
(2)求几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解贵州省某州2020届高三理科生的化学成绩的情况,该州教育局组织高三理科生进行了摸底考试,现从参加考试的学生中随机抽取了100名理科生,,将他们的化学成绩(满分为100分)分为![]()
![]()
![]()
![]()
![]()
![]() 6组,得到如图所示的频率分布直方图.
6组,得到如图所示的频率分布直方图.

(1)求a的值;
(2)记A表示事件“从参加考试的所有理科生中随机抽取一名学生,该学生的化学成绩不低于70分”,试估计事件A发生的概率;
(3)在抽取的100名理科生中,采用分层抽样的方法从成绩在![]() 内的学生中抽取10名,再从这10名学生中随机抽取4名,记这4名理科生成绩在
内的学生中抽取10名,再从这10名学生中随机抽取4名,记这4名理科生成绩在![]() 内的人数为X,求X的分布列与数学期望.
内的人数为X,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是各项均不为0的等差数列,公差为
是各项均不为0的等差数列,公差为![]() ,
,![]() 为其前
为其前![]() 项和,且满足
项和,且满足![]() .数列
.数列![]() 满足
满足![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1)求![]() ;
;
(2)求![]() ;
;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 过点
过点![]() ,左焦点
,左焦点![]()
(1)求椭圆C的标准方程;
(2)过点F作于x轴不重合的直线l,l与椭圆交于A,B两点,点A在直线![]() 上的投影N与点B的连线交x轴于D点,D点的横坐标
上的投影N与点B的连线交x轴于D点,D点的横坐标![]() 是否为定值?若是,请求出定值;若不是,请说明理由
是否为定值?若是,请求出定值;若不是,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.

(I)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(II)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com