解:(1)由f(x)═x
2-alnx得:f′(x)=
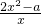
,由g(x)=
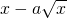
得:g′(x)=
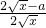
.
又由题意可得f′(1)=g′(1),即2-a=

,
故a=2,所以f(x)=x
2-2lnx,g(x)=x-2

;
(2)h(x)=f(x)-g(x)=x
2-x-2lnx+2

得:
h′(x)=2x-1-

+

=
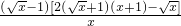
,
由x>0可知:2(

+1)(x+1)-

>0.
故当x∈(0,1)时,h′(x)<0,h(x)递减,当x∈(1,+∞)时,h′(x)>0,h(x)递增,
所以函数h(x)的最小值为h(1)=1
2-1-2ln1+2

=2;
(3)当x∈(0,4)时,g(x)=x-2

=
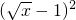
-1<0,,而f(x)=x
2-2lnx≥1,
当m≥0时,不等式f(x)≥m•g(x)在x∈(0,4)均成立.
当m<0时,m•g(x)的最大值为m•g(1)=-m,
故要使f(x)≥m•g(x)恒成立,则必需-m≤1,,即m≥-1.
事实上,当x=1时,m=-1.故可知此时-1≤m<0.
综上可知当m≥-1时,不等式f(x)≥m•g(x)在x∈(0,4)均成立.
分析:(1)求出f(x)的导函数,求出g(x)的导函数,由两函数的图象交直线x=1且曲线y=f(x)在点A处的切线与曲线y=g(x)在点B处的切线平行,得到x=1时,两导函数的值相等,即可列出关于a的方程,求出方程的解即可得到a的值,把a的值代入即可确定出f(x)和g(x)的表达式;
(2)把(1)中确定出的f(x)和g(x)代入即可确定出h(x),求出h(x)的导函数,根据负数没有对数及平方根得到x大于0,然后分x大于0小于1和x大于1两种情况讨论导函数的正负,即可得到函数h(x)的单调性,根据函数的增减性即可得到h(x)的最小值;
(3)由x的范围,得到g(x)小于0,f(x)大于1,所以当m大于等于0时,不等式f(x)≥m•g(x)在x∈(0,4)均成立;当m小于0时,求出mg(x)的最大值为-m,不等式要恒成立,即要-m小于等于1,即可求出此时m的范围,综上,得到不等式恒成立时m的范围.
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,掌握不等式恒成立时满足的条件及导数在最大值、最小值问题中的应用,是一道中档题.

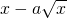 的图象分别交直线x=1于点A,B,且曲线y=f(x)在点A处的切线与曲线y=g(x)在点B处的切线平行.
的图象分别交直线x=1于点A,B,且曲线y=f(x)在点A处的切线与曲线y=g(x)在点B处的切线平行.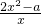 ,由g(x)=
,由g(x)=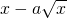 得:g′(x)=
得:g′(x)=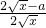 .
. ,
, ;
; 得:
得: +
+ =
=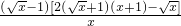 ,
, +1)(x+1)-
+1)(x+1)- >0.
>0. =2;
=2; =
=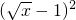 -1<0,,而f(x)=x2-2lnx≥1,
-1<0,,而f(x)=x2-2lnx≥1,

 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案