Question

若函数f（x）=x³+ax+b有三个零点，分别为x₁，x₂，x₃，且满足x₁＜1，x₂=1，x₃＞1，则实数a的取值范围是

1. A.
   （-∞，0）
2. B.
   （-∞，-1）
3. C.
   （-∞，-2）
4. D.
   （-∞，-3）

Answer 1

D
分析：利用函数零点的取值可以判断，
解答：因为x₂=1，所以f（1）=a+b=0，即b=-a，
所以f（x）=x³+ax+b=x³+ax+-a．
函数导数为f'（x）=3x²+a，因为f（x）=x³+ax+b有三个零点，所以f'（x）=0，有两个不等的实根，所以a＜0．
则由f'（x）=0得x═．
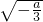
即当x=函数取得极大值，当x=时，函数取得极小值．
因为x₁＜1，x₃＞1，
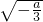
所以＞1，解得a＜-3．
故选D．
点评：本题主要考查函数的零点的应用，以及利用导数研究函数的极值问题，要求熟练掌握导数和极值之间的关系．