Question

20．若P是等边三角形ABC所在平面外一点，且PA=PB=PC，D，E，F分别是AB，BC，CA的中点，则下列结论中不正确的是（　　）

• A． BC∥平面PDF
• B． DF⊥平面PAE
• C． 平面PAE⊥平面ABC
• D． 平面PDF⊥平面ABC

Answer 1

分析 由DF∥BC，得BC∥平面PDF；由PE⊥BC，AE⊥BC，DF∥BC，得DF⊥平面PAE；由BC⊥平面PAE，得平面PAE⊥平面ABC；设AE∩DF=O，由PO与平面ABC不垂直，得平面PDF与平面ABC不垂直．

解答 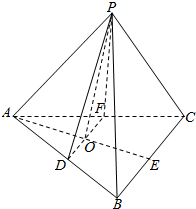解：∵P是等边三角形ABC所在平面外一点，且PA=PB=PC，
D，E，F分别是AB，BC，CA的中点，
∴DF∥BC，
∵DF?平面PDF，BC?平面PDF，∴BC∥平面PDF，故A正确；
∵PA=PB=PC，E是BC中点，
∴PE⊥BC，AE⊥BC，
∵PE∩AE=E，∴BC⊥平面PAE，
∵DF∥BC，∴DF⊥平面PAE，故B正确；
∵BC⊥平面PAE，BC?平面ABC，
∴平面PAE⊥平面ABC，故C正确；
设AE∩DF=O，连结PO，∵O不是等边三角形ABC的重心，∴PO与平面ABC不垂直，
∴平面PDF与平面ABC不垂直，故D错误．
故选：D．

点评 本题考查命题真假的判断，是中档题，解题时要认真审题，注意空间思维能力的培养．