
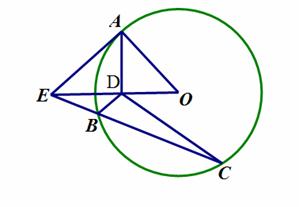
如图,AE是圆O的切线,A是切点,AD⊥OE于D, 割线EC交圆O于B、C两点.
(Ⅰ)证明:O,D,B,C四点共圆;
(Ⅱ)设∠DBC=50°,∠ODC=30°,求∠OEC的大小.
科目:高中数学 来源: 题型:
为了估计某水池中鱼的尾数,先从水池中捕出2000尾鱼,并给每尾鱼做上标记(不影响存活),然后放回水池,经过适当的时间,再从水池中捕出500尾鱼,其中有标记的鱼为40尾,根据上述数据估计该水池中鱼的尾数为
A.10000B.20000 C.25000D.30000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com