练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一半径为的水轮,水轮圆心距离水面2,已知水轮每分钟转动(按逆时针方向)3圈,当水轮上点从水中浮现时开始计时,即从图中点开始计算时间.

    (1)当秒时点离水面的高度_________；

    (2)将点距离水面的高度(单位: )表示为时间(单位: )的函数，则此函数表达式为_______________ .

    【答案】

    【解析】

    1利用直角三角形的边角关系，即可求出5秒后点P离开水面的距离；2由题意求值，结合的情况可求出的值，即得函数解析式．

    解：1秒时，水轮转过角度为，

    在中，，；

    在中，，，

    此时点离开水面的高度为；

    2由题意可知，，

    设角是以Ox为始边，为终边的角，

    由条件得，其中；

    将，代入，得，

    ；

    所求函数的解析式为．

    故答案为：1，2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知某种细菌的适宜生长温度为，为了研究该种细菌的繁殖数量（单位：个）随温度（单位：）变化的规律，收集数据如下：

    温度/

    12

    14

    16

    18

    20

    22

    24

    繁殖数量/个

    20

    25

    33

    27

    51

    112

    194

    对数据进行初步处理后，得到了一些统计量的值，如下表所示：

    18

    66

    3.8

    112

    4.3

    1428

    20.5

    其中，.

    （1）请绘出关于的散点图，并根据散点图判断与哪一个更适合作为该种细菌的繁殖数量关于的回归方程类型（结果精确到0.1）；

    （2）当温度为时，该种细菌的繁殖数量的预报值为多少？

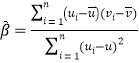    参考公式：对于一组数据，其回归线的斜率和截距的最小二乘估计分别为：，.参考数据：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的一个顶点是，离心率为．

    （Ⅰ）求椭圆的方程；

    （Ⅱ）已知矩形的四条边都与椭圆相切，设直线AB方程为，求矩形面积的最小值与最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆心为的圆经过点和，且圆心在直线轴上．

    （Ⅰ）求圆的方程；

    （Ⅱ）过点的动直线与圆相交于，两点．当时，求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，平面平面，，,，，，分别为的中点.

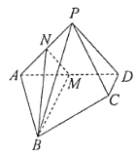
    （Ⅰ）证明：平面∥平面；

    （Ⅱ）若，

    （1）求平面与平面所成锐二面角的余弦值；

    （2）求点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在点处的切线与直线平行．

    （Ⅰ）求实数的值；

    （Ⅱ）设．

    （i）若函数在上恒成立，求的最大值；

    （ii）当时，判断函数有几个零点，并给出证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一半径为的水轮,水轮圆心距离水面2,已知水轮每分钟转动(按逆时针方向)3圈,当水轮上点从水中浮现时开始计时,即从图中点开始计算时间.

    (1)当秒时点离水面的高度_________；

    (2)将点距离水面的高度(单位: )表示为时间(单位: )的函数，则此函数表达式为_______________ .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在下列四个几何体中，它们的三视图（主视图、左视图、俯视图）中有且仅有两个相同，而另一个不同的几何体是（ ）

    （1）棱长为1的正方体

    （2）底面直径和高均为1的圆柱

    （3）底面直径和高均为1的圆锥

    （4）底面边长为1、高为2的正四棱柱

    A.（2）（3）（4）B.（1）（2）（3）

    C.（1）（3）（4）D.（1）（2）（4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知点，过直线左侧的动点作于点的角平分线交轴于点，且，记动点的轨迹为曲线．

    （1）求曲线的方程；

    （2）过点作直线交曲线于两点，点在上，且轴，试问：直线是否恒过定点？请说明理由．

    查看答案和解析>>

    同步练习册答案