Question

3．若不等式组$\left\{\begin{array}{l}{|x|+|y|≤3}\\{y+3≤k（x+1）}\end{array}\right.$表示的平面区域是三角形，则实数k的取值范围是（　　）

• A． -$\frac{3}{2}$＜k≤$\frac{3}{4}$
• B． k＜-$\frac{3}{2}$或k≥$\frac{3}{4}$
• C． -$\frac{3}{2}$＜k＜0或k≥$\frac{3}{4}$
• D． k＜-$\frac{3}{2}$或0＜k≤$\frac{3}{4}$

Answer 1

分析 画出图形，y+3=k（x+1）表示一条经过点M（-1，-3）、斜率等于k的直线，当斜率k满足大于零且小于或等于MC的斜率、或者斜率k满足小于MA的斜率时，表示的平面区域是三角形，求出MC、MA的斜率即可求得实数k的取值范围．

解答 解：如图所示：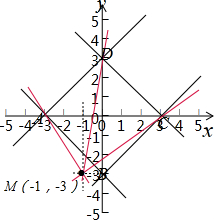
，
由于|x|+|y|表示正方形ABCD内部区域，包含边界．
而y+3=k（x+1）表示一条经过点M（-1，-3）、斜率等于k的直线．
故当斜率k满足大于零且小于或等于MC的斜率、或者斜率k满足小于MA的斜率时，表示的平面区域是三角形．
而MC的斜率等于$\frac{3}{4}$，MA的斜率等于-$\frac{3}{2}$，
故应有 0＜k≤$\frac{3}{4}$，或k≤-$\frac{3}{2}$，
故选：D．

点评 本题主要考查直线过定点问题，二元一次不等式组表示平面区域，体现了数形结合的数学思想，属于基础题．