
(本小题满分14分) 函数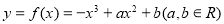 .
.
(1)要使 在(0,1)上单调递增,求
在(0,1)上单调递增,求 的取值范围;
的取值范围;
(2)当 >0时,若函数满足
>0时,若函数满足 =1,
=1,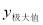 =
=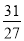 ,求函数
,求函数 的解析式;
的解析式;
(3)若x∈[0,1]时, 图象上任意一点处的切线倾斜角为θ,求当0≤θ≤
图象上任意一点处的切线倾斜角为θ,求当0≤θ≤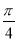 时
时 的取值范围.
的取值范围.
(1) ≥
≥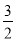 ;(2)
;(2)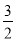 ≤
≤ ≤
≤ .
.
【解析】
试题分析:(1)若可导函数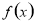 在指定的区间
在指定的区间 上单调递增(减),求参数问题,可转化为
上单调递增(减),求参数问题,可转化为
 恒成立,从而构建不等式,要注意“=”是否可以取到.(2)已知可导函数的极值求函数解析式的步骤一、求导数
恒成立,从而构建不等式,要注意“=”是否可以取到.(2)已知可导函数的极值求函数解析式的步骤一、求导数 ;二、求方程
;二、求方程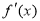
 的根;三、检查
的根;三、检查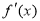 与方程
与方程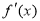
 的根左右值的符号,如果左正右负,那么
的根左右值的符号,如果左正右负,那么 在这个根处取得极大值,如果左负右正,那么
在这个根处取得极大值,如果左负右正,那么 在这个根处取得极小值,四、再根据所给的极值,列出方程(或方程组)求出参数即可;(3)导数的几何意义的应用.
在这个根处取得极小值,四、再根据所给的极值,列出方程(或方程组)求出参数即可;(3)导数的几何意义的应用.
试题解析:(1) ,要使
,要使 在(0,1)上单调递增,
在(0,1)上单调递增,
则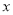 ∈(0,1)时,
∈(0,1)时,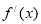 ≥0恒成立.∴
≥0恒成立.∴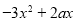 ≥0,即当
≥0,即当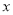 ∈(0,1)时,
∈(0,1)时, ≥
≥ 恒成立.
恒成立.
∴ ≥
≥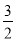 ,即
,即 的取值范围是[
的取值范围是[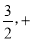 ∞
∞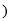 . 4分
. 4分
(2)由 ,令
,令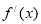 =0,得
=0,得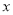 =0,或
=0,或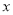 =
=
 .∵
.∵ >0,∴当
>0,∴当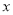 变化时,
变化时,
 、
、 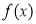 的变化情况如下表:
的变化情况如下表:
| (-∞,0) | 0 | (0, |
| ( |
| - | 0 | + | 0 | - |
|
| 极小值 |
| 极大值 |
|
∴y极小值=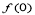 =b=1,y极大值=
=b=1,y极大值= = -
= -
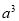 +
+ 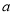 ·
·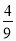
 +1=
+1= .
.
∴b=1,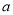 =1.故
=1.故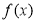 =
=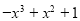 . 9分
. 9分
(3)当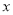 ∈[0,1]时,tanθ=
∈[0,1]时,tanθ= .由θ∈[0,
.由θ∈[0, ],得0≤
],得0≤ ≤1,
≤1,
即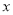 ∈[0,1]时,0≤
∈[0,1]时,0≤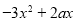 ≤1恒成立.当
≤1恒成立.当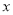 =0时,
=0时, ∈R.
∈R.
当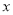 ∈(0,1]时,由
∈(0,1]时,由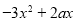 ≥0恒成立,由(2)知
≥0恒成立,由(2)知 ≥
≥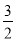 .
.
由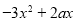 ≤1恒成立,
≤1恒成立, ≤
≤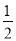 (3
(3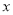 +
+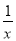 ),∴
),∴ ≤
≤ (等号在
(等号在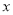 =
= 时取得).
时取得).
综上,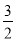 ≤
≤ ≤
≤ . 14分
. 14分
考点:函数的极值,单调性与导数,函数导数的几何意义.


科目:高中数学 来源:2015届青海省西宁市高三上学期第一次月考理科数学试卷(解析版) 题型:选择题
三棱锥的三视图如图,正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形,则此三棱锥的体积为( )
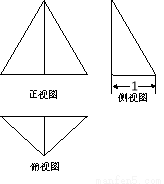
A.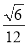 B.
B.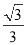 C.
C.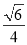 D.
D.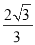
查看答案和解析>>
科目:高中数学 来源:2015届陕西南郑中学高二下学期期末考试理科数学试卷(解析版) 题型:选择题
条件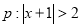 ,条件
,条件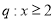 ,则
,则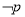 是
是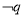 的( )
的( )
A.充分非必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要的条件
查看答案和解析>>
科目:高中数学 来源:2015届陕西南郑中学高二下学期期末考试文科数学试卷(解析版) 题型:解答题
已知向量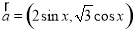 ,
,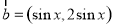 ,函数
,函数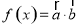
(1)求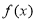 的单调递增区间;
的单调递增区间;
(2)若不等式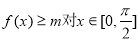 都成立,求实数m的最大值.
都成立,求实数m的最大值.
查看答案和解析>>
科目:高中数学 来源:2015届陕西南郑中学高二下学期期末考试文科数学试卷(解析版) 题型:填空题
在10000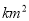 的海域中有40
的海域中有40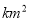 的大陆架贮藏着石油,假如在海域中任意一点钻探,钻到油层面的概率是 .
的大陆架贮藏着石油,假如在海域中任意一点钻探,钻到油层面的概率是 .
查看答案和解析>>
科目:高中数学 来源:2016届福建省高一下学期期中考试数学试卷(解析版) 题型:解答题
下面是计算应纳税所得额的算法过程,其算法如下:
第一步 输入工资x(注x<=5000);
第二步 如果x<=800,那么y=0;如果800<x<=1300,那么 y=0.05(x-800);
否则 y=25+0.1(x-1300)
第三步 输出税款y, 结束.
请写出该算法的程序框图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com