
已知向量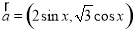 ,
,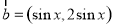 ,函数
,函数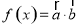
(1)求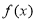 的单调递增区间;
的单调递增区间;
(2)若不等式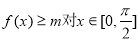 都成立,求实数m的最大值.
都成立,求实数m的最大值.
(1)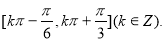 (2)0
(2)0
【解析】
试题分析:(1)求解较复杂三角函数的单调区间时,首先化成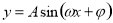 形式,再
形式,再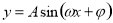 的单调区间,只需把
的单调区间,只需把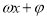 看作一个整体代入
看作一个整体代入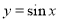 相应的单调区间,注意先把
相应的单调区间,注意先把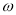 化为正数,这是容易出错的地方.,(2)求解较复杂三角函数的最值时,首先化成
化为正数,这是容易出错的地方.,(2)求解较复杂三角函数的最值时,首先化成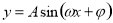 形式,在求最大值或最小值,寻求角与角之间的关系,化非特殊角为特殊角;正确灵活运用公式,通过三角变换消去或约去一些非特殊角的三角函数值,注意题中角的范围;(3)对于恒成立的问题,常用到以下两个结论:1)
形式,在求最大值或最小值,寻求角与角之间的关系,化非特殊角为特殊角;正确灵活运用公式,通过三角变换消去或约去一些非特殊角的三角函数值,注意题中角的范围;(3)对于恒成立的问题,常用到以下两个结论:1)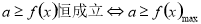 ,2)
,2)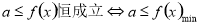
试题解析:(1)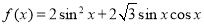
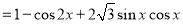
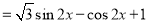
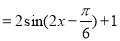
由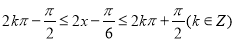 ,
,
得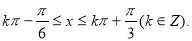
所以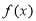 的单调增区间是
的单调增区间是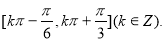 6分
6分
(2)因为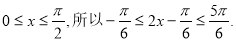
所以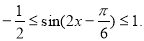
所以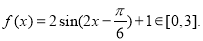 所以
所以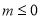 ,
,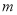 的最大值为0 12分.
的最大值为0 12分.
考点:三角函数的化简;求三角函数,单调性及最值.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源:2015届陕西省西安市高二上学期期中考试数学试卷(解析版) 题型:选择题
在数列1,1,2,3,5,8,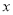 ,21,34,55中,
,21,34,55中,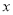 等于( )
等于( )
A.11 B.12 C.13 D.14
查看答案和解析>>
科目:高中数学 来源:2015届陕西南郑中学高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知双曲线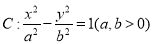 的左、右焦点分别为
的左、右焦点分别为
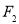 ,过
,过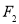 作双曲线
作双曲线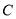 的一条渐近线的垂线,垂足为
的一条渐近线的垂线,垂足为 ,若
,若 的中点
的中点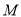 在双曲线
在双曲线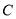 上,则双曲线
上,则双曲线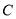 的离心率为( )
的离心率为( )
A. B.
B.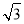 C.2 D.3
C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2015届陕西南郑中学高二下学期期末考试文科数学试卷(解析版) 题型:解答题
(本小题满分14分) 函数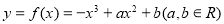 .
.
(1)要使 在(0,1)上单调递增,求
在(0,1)上单调递增,求 的取值范围;
的取值范围;
(2)当 >0时,若函数满足
>0时,若函数满足 =1,
=1,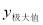 =
=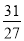 ,求函数
,求函数 的解析式;
的解析式;
(3)若x∈[0,1]时, 图象上任意一点处的切线倾斜角为θ,求当0≤θ≤
图象上任意一点处的切线倾斜角为θ,求当0≤θ≤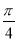 时
时 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016届福建省高一下学期期中考试数学试卷(解析版) 题型:填空题
在大小相同的6个球中,2个是红球,4个是白球,若从中任意选取3个,则所选的3个球中至少有1个红球的概率是___________;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com