
【题目】已知从有限个平面向量构成的集合![]() 中任取三个元素,其中总存在两个元素
中任取三个元素,其中总存在两个元素![]() ,使得
,使得![]() .试求
.试求![]() 中元素个数的最大值.
中元素个数的最大值.
【答案】7
【解析】
所求![]() 中元素个数的最大值为7.
中元素个数的最大值为7.
设点![]() 、
、![]() 、
、![]() 是平面上任意三点,考虑7元集合
是平面上任意三点,考虑7元集合![]() ,它显然满足条件.下面证明:
,它显然满足条件.下面证明:![]() 中的元素不能多于7个.
中的元素不能多于7个.
当![]() 中的元素全部共线时,将所有元素的起点移至同一点,作一条与所有元素平行的直线
中的元素全部共线时,将所有元素的起点移至同一点,作一条与所有元素平行的直线![]() 并作出
并作出![]() 中所有元素在直线
中所有元素在直线![]() 上的投影,于是,
上的投影,于是,![]() 中的所有向量均对应以
中的所有向量均对应以![]() 中元素的共同起点在
中元素的共同起点在![]() 上的投影为原点,直线
上的投影为原点,直线![]() 的任意取定一个方向为正方向的数轴上的坐标.从而,问题可转化为求与原题对应的数集问题(由二维转化为一维).
的任意取定一个方向为正方向的数轴上的坐标.从而,问题可转化为求与原题对应的数集问题(由二维转化为一维).
接下来证明:该数集中至多有7个元素.
首先证明:该数集中最多有3个正数.假设可能有不少于4个的元素是正数,其中,最大的4个数分别为![]() 、
、![]() 、
、![]() 、
、![]() ,且
,且![]() .
.
事实上,![]() ,所以,和数
,所以,和数![]() .而大于
.而大于![]() 的元素只有
的元素只有![]() 一个,却有
一个,却有![]() ,于是,在集合
,于是,在集合![]() 或
或![]() 中,至少有一个集合的任意两个元素之和不在
中,至少有一个集合的任意两个元素之和不在![]() 中.这与已知矛盾,故该数集中最多有3个正数.同理,该数集中最多有3个负数.加上一个0,从而,数集
中.这与已知矛盾,故该数集中最多有3个正数.同理,该数集中最多有3个负数.加上一个0,从而,数集![]() 中至多有7个元素.
中至多有7个元素.
当![]() 中的元素不全共线时,将所有元素的起点移至同一点
中的元素不全共线时,将所有元素的起点移至同一点![]() ,由
,由![]() 的有限性知可作出平面直角坐标系
的有限性知可作出平面直角坐标系![]() ,使得
,使得![]() 中的元素均不与坐标轴平行.
中的元素均不与坐标轴平行.
下面证明:上半平面内至多有3个元素.
首先证明:上半平面的所有元素全不共线.假设上半平面内存在![]() 中的元素
中的元素![]() 与
与![]() 共线,则可取与
共线,则可取与![]() 和
和![]() 夹角最小的元素
夹角最小的元素![]() .考虑集合
.考虑集合![]() ,由
,由![]() 的取法,知
的取法,知![]() 和
和![]() 均不在
均不在![]() 中(两向量的和向量在这两个向量之间).于是,
中(两向量的和向量在这两个向量之间).于是,![]() 中存在
中存在![]() ,使得
,使得![]() ,从而,
,从而,![]() 与
与![]() 、
、![]() 共线.考虑集合
共线.考虑集合![]() ,类似上面的讨论,知
,类似上面的讨论,知![]() 中存在
中存在![]() 与
与![]() 、
、![]() 共线.如此讨论下去,知
共线.如此讨论下去,知![]() 中存在无穷多个元素与
中存在无穷多个元素与![]() 、
、![]() 共线,矛盾.故上半平面的所有元素全不共线.
共线,矛盾.故上半平面的所有元素全不共线.
其次证明:上半平面内至多有3个元素.假设在上半平面内有不少于4个元素,按逆时针方向顺次取其中4个相邻元素![]() 、
、![]() 、
、![]() 、
、![]() .考虑集合
.考虑集合![]() ,则有
,则有![]() ;考虑集合
;考虑集合![]() ,则有
,则有![]() .从而,
.从而,![]() ,即
,即![]() .这与
.这与![]() 、
、![]() 同在上半平面内矛盾,故上半平面内至多有3个元素.同理,下半平面内至多有3个元素.加上零向量,从而,集合
同在上半平面内矛盾,故上半平面内至多有3个元素.同理,下半平面内至多有3个元素.加上零向量,从而,集合![]() 中至多有7个元素.
中至多有7个元素.
综上所述,集合![]() 中元素个数的最大值为7.
中元素个数的最大值为7.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
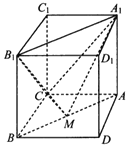
【题目】如图,在棱长为2的正方体![]() 中,M是线段AB上的动点.
中,M是线段AB上的动点.
![]() 证明:
证明:![]() 平面
平面![]() ;
;
![]() 若点M是AB中点,求二面角
若点M是AB中点,求二面角![]() 的余弦值;
的余弦值;
![]() 判断点M到平面
判断点M到平面![]() 的距离是否为定值?若是,求出定值;若不是,请说明理由.
的距离是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,右焦点
,右焦点![]() 到直线
到直线![]() :
:![]() 的距离为
的距离为![]() .
.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 过椭圆右焦点
过椭圆右焦点![]() 斜率为
斜率为![]() 的直线l与椭圆C相交于E、F两点,A为椭圆的右顶点,直线AE,AF分别交直线
的直线l与椭圆C相交于E、F两点,A为椭圆的右顶点,直线AE,AF分别交直线![]() 于点M,N,线段MN的中点为P,记直线
于点M,N,线段MN的中点为P,记直线![]() 的斜率为
的斜率为![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一士兵要在一个半径为![]() 的圆形区域内检查是否埋有地雷,他所用的检查仪器的有效作用范围的半径为
的圆形区域内检查是否埋有地雷,他所用的检查仪器的有效作用范围的半径为![]() .求该士兵从该圆边界上一点
.求该士兵从该圆边界上一点![]() 出发,至少需走多少米才能将区域检测完,且回到出发点?
出发,至少需走多少米才能将区域检测完,且回到出发点?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医疗研究所为了检验某种血清预防感冒的作用,把![]() 名使用血清的人与另外
名使用血清的人与另外![]() 名未用血清的人一年中的感冒记录作比较,提出假设
名未用血清的人一年中的感冒记录作比较,提出假设![]() :“这种血清不能起到预防感冒的作用”,利用
:“这种血清不能起到预防感冒的作用”,利用![]() 列联表计算得
列联表计算得![]() ,经查对临界值表知
,经查对临界值表知![]() .对此,四名同学做出了以下的判断:
.对此,四名同学做出了以下的判断:
![]() :有
:有![]() 的把握认为“这种血清能起到预防感冒的作用”
的把握认为“这种血清能起到预防感冒的作用”
![]() :若某人未使用该血清,那么他在一年中有
:若某人未使用该血清,那么他在一年中有![]() 的可能性得感冒
的可能性得感冒
![]() :这种血清预防感冒的有效率为
:这种血清预防感冒的有效率为![]()
![]() :这种血清预防感冒的有效率为
:这种血清预防感冒的有效率为![]()
则下列结论中,正确结论的序号是
①![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国人旅游有个特点:喜欢在旅游区购买当地的名优土特产,黄冈市有很多名优土特产,黄冈市的蕲春县就有闻名于世的“蕲春四宝”![]() 蕲竹、蕲艾、蕲蛇、蕲龟
蕲竹、蕲艾、蕲蛇、蕲龟![]() ,由于医圣李时珍出生在蕲春县,很多人慕名而来,回家时顺带买点“蕲春四宝”,通过随机询问60名不同性别的游客在购买“蕲春四宝”时是否在来蕲春县之前就知道“蕲春四宝”,得到如下列联表:
,由于医圣李时珍出生在蕲春县,很多人慕名而来,回家时顺带买点“蕲春四宝”,通过随机询问60名不同性别的游客在购买“蕲春四宝”时是否在来蕲春县之前就知道“蕲春四宝”,得到如下列联表:
男 | 女 | 总计 | |
事先知道“蕲春四宝” | 8 | n | q |
事先不知道“蕲春四宝” | m | 4 | 36 |
总计 | 40 | p | t |
|
|
|
|
|
|
|
|
附:![]()
![]() 写出列联表中各字母代表的数字;
写出列联表中各字母代表的数字;
![]() 由以上列联表判断,能否在犯错误的概率不超过
由以上列联表判断,能否在犯错误的概率不超过![]() 的前提下认为购买“蕲春四宝”和是否“事先知道
的前提下认为购买“蕲春四宝”和是否“事先知道![]() 蕲春四宝
蕲春四宝![]() 有关系”?
有关系”?
![]() 现从这60名游客中用分层抽样的方法抽取15名游客进行问卷调查,再从抽取的女游客中,随机选出2人给予小礼品,求有2名女游客是事先知道“蕲春四宝”的概率?
现从这60名游客中用分层抽样的方法抽取15名游客进行问卷调查,再从抽取的女游客中,随机选出2人给予小礼品,求有2名女游客是事先知道“蕲春四宝”的概率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com