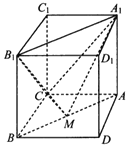
【题目】如图，在棱长为2的正方体
中，M是线段AB上的动点．
证明：
平面
；
若点M是AB中点，求二面角
的余弦值；
判断点M到平面的距离是否为定值？若是，求出定值；若不是，请说明理由．
【答案】（1）证明见解析；（2）
；（3）点
到平面
的距离为定值
.
【解析】
（1）利用正方体的性质得
，由线面平行的判定定理证明即可.（2）建立空间直角坐标系
求出平面
和平面
的法向量
，利用向量的夹角公式求出二面角的余弦值，即可得解.（3）由（1）得点到平面的距离等于
上任意一点到平面的距离，结合（2）和点到面的距离公式得点到平面的距离即可.
（1）证明：因为在正方体
中，，
平面，
平面，
平面
（2）
在正方体中，
，
，
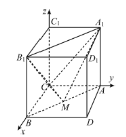
两两互相垂直，则建立空间直角坐标系
如图所示，则
，
，
，
，所以
，
，
，
，设向量
，
分别为平面和平面的法向量，由
取
，则
，
，
.
同理
取
，则
，
，
.
，
又二面角
的平面角为锐角，
二面角的余弦值为
（3）由（1）知
平面
.点到平面的距离等于上任意一点到平面的距离，取点为
，结和（2）和点到平面的距离
.点到平面的距离定值为
一本好题口算题卡系列答案科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率
，左、右焦点分别为
，点
，点
在线段
的中垂线上．
（1）求椭圆
的方程；
（2）设直线
与椭圆
交于
两点，直线
与
的倾斜角分别为
，且
，求证：直线
过定点，并求该定点的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2017年“十一”期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（
）分成六段： 
， 
， 
， 
， 
， 
，后得到如图的频率分布直方图．
（1）求这40辆小型车辆车速的众数和中位数的估计值；
（2）若从车速在
的车辆中任抽取2辆，求车速在的车辆恰有一辆的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，一辆汽车从A市出发沿海岸一条笔直公路以
的速度向东匀速行驶，汽车开动时，在A市南偏东方向距A市500km且与海岸距离为300km的海上B处有一艘快艇与汽车同时出发，要把一份文件交给这辆汽车的司机．
（1）快艇至少以多大的速度行驶才能把文件送到司机手中？
（2）求快艇以最小速度行驶时的行驶方向与
所成角的大小．
（3）若快艇每小时最快行驶
，快艇应如何行驶才能尽快把文件交到司机手中？最快需多长时间？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】销售甲、乙两种商品所得利润分别是
万元，它们与投入资金
万元的关系分别为
，
，（其中
都为常数），函数对应的曲线
、
如图所示．
（1）求函数
与
的解析式；
（2）若该商场一共投资4万元经销甲、乙两种商品，求该商场所获利润的最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
