Question

【题目】已知函数。

（Ⅰ）求函数的单调区间；

（Ⅱ）若函数在上是减函数，求实数的取值范围。

Answer 1

【答案】(1) 函数f(x)的单调递减区间是(0， )；单调递增区间是(，＋∞);(2) a≤－.

【解析】试题分析：（Ⅰ）先求出函数的导数，再通过讨论a的范围，从而求出其单调区间，（Ⅱ）由g(x)＝＋x2＋2aln x得g′(x)＝－＋2x＋，建立新函数，求出其最小值，解出即可．

试题解析：

（Ⅰ）函数f(x)的定义域为(0，＋∞).

①当a≥0时，f′(x)＞0，f(x)的单调递增区间为(0，＋∞)；

②当a＜0时，f′(x)＝.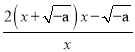

当x变化时，f′(x)，f(x)的变化情况如下：

x	(0， )		(，＋∞)
f′(x)	－	0	＋
f(x)		极小值

由上表可知，函数f(x)的单调递减区间是(0， )；单调递增区间是(，＋∞).

（Ⅱ ）由g(x)＝＋x2＋2aln x，得g′(x)＝－＋2x＋，

由已知函数g(x)为[1,2]上的单调减函数，则g′(x)≤0在[1,2]上恒成立，

即－＋2x＋≤0在[1,2]上恒成立．即a≤－x2在[1,2]上恒成立.

令，则h′(x)＝－－2x＝－(＋2x)

，所以h(x)在[1,2]上为减函数，

h(x)min＝h(2)＝－， 所以a≤－.