
已知矩阵 , (1)求逆矩阵
, (1)求逆矩阵 ;(2)若矩阵
;(2)若矩阵 满足
满足 ,试求矩阵
,试求矩阵 .
.
科目:高中数学 来源: 题型:解答题
设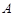 是由
是由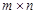 个实数组成的
个实数组成的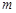 行
行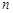 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(1)数表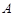 如表1所示,若经过两“操”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);表1
如表1所示,若经过两“操”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);表1
| 1 | 2 | 3 | 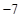 |
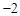 | 1 | 0 | 1 |
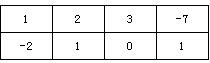
 如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数
如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数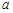 的所有可能值;表2
的所有可能值;表2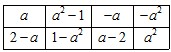
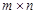 个实数组成的
个实数组成的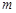 行
行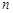 列的任意一个数表
列的任意一个数表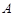 ,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负实数?请说明理由.
,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负实数?请说明理由. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,四边形ABCD和四边形AB′C′D分别是矩形和平行四边形,其中各点的坐标分别为A(-1,2)、B(3,2)、C(3,-2)、D(-1,-2)、B′(3,7)、C′(3,3).求将四边形ABCD变成四边形AB′C′D的变换矩阵M.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com