
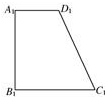
 如图,已知四边形ABCD的直观图是直角梯形A1B1C1D1,且A1B1=B1C1=2A1D1=4,则四边形ABCD的面积为( )
如图,已知四边形ABCD的直观图是直角梯形A1B1C1D1,且A1B1=B1C1=2A1D1=4,则四边形ABCD的面积为( )| A. | 12 | B. | 12$\sqrt{2}$ | C. | 24$\sqrt{2}$ | D. | 24 |
分析 如图,取∠GB1C1=135°,确定平面图形的形状,求出底边边长,上底边边长,以及高,然后求出面积.
解答 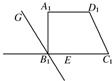 解:如图,取∠GB1C1=135°,过点A1作A1E∥GB1,
解:如图,取∠GB1C1=135°,过点A1作A1E∥GB1,
易求得B1E=4,A1E=4$\sqrt{2}$,故以B1C1和B1A1为坐标轴建立直角坐标系,由直观图原则,B,C与B1,C1重合,然后过点E作B1A1的平行线,且使得AE=2A1E=8$\sqrt{2}$,
即得点A,然后过A作AD∥BC且使得AD=2,
即四边形ABCD上底和下底边长分别为2,4,高为8$\sqrt{2}$,
故其面积S=$\frac{1}{2}$(2+4)×8$\sqrt{2}$=24$\sqrt{2}$.
故选:C.
点评 本题考查平面图形的直观图,考查计算能力,作图能力,是基础题.


 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{x+1}$ | B. | y=(x-2)2 | C. | y=3-x | D. | y=log0.1(x+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{{1+cos{{120}°}}}{2}}$ | B. | ${cos^2}\frac{π}{12}-{sin^2}\frac{π}{12}$ | ||
| C. | cos42°sin12°-sin42°cos12° | D. | $\frac{{tan{{15}°}}}{{1-{{tan}^2}{{15}°}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com