
分析 (1)由p为真命题,得0<m<5,m∈N+,分别化简集合A,B.当0<m<4,m∈N+时,B⊆A,可得A∩B=B.当m=4时,A⊆B,A∩B=A,即可得出.
(2)由p且q为真命题,可得p为真命题,q为真命题,即“x∈A”是“x∈B”的必要不充分条件,因此集合B是集合A的真子集,即可得出.
解答 解:(1)由p为真命题,得0<m<5,m∈N+,
则集合A={x|m<$\frac{1-x}{x}$}=$\{x|0<x<\frac{1}{m+1}\}$.
又B={x|lo${g}_{\frac{1}{2}}$x>2}={x|$0<x<\frac{1}{4}$}.
当0<m<4,m∈N+时,B⊆A,
∴A∩B=B={x|$0<x<\frac{1}{4}$}.
当m=4时,A⊆B,所以A∩B=A=$\{x|0<x<\frac{1}{5}\}$.
(2)∵p且q为真命题,
∴p为真命题,q为真命题,
即“x∈A”是“x∈B”的必要不充分条件,
∴集合B是集合A的真子集,
∴$\frac{1}{m+1}>\frac{1}{4}$且0<m<5,m∈N+,
解得:m=1或m=2.
点评 本题考查了简易逻辑的判定、集合的运算性质、不等式的解法、函数的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 已知函数f(x)=sin(ωx-$\frac{π}{4}$)(ω>0,x∈R)的最小正周期为π.
已知函数f(x)=sin(ωx-$\frac{π}{4}$)(ω>0,x∈R)的最小正周期为π.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{π}{3}$个单位长度 | D. | 向右平移$\frac{π}{3}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2<x≤1} | B. | {x|1<x<2} | C. | {x|1<x≤2} | D. | {x|-1≤x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
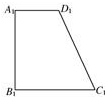 如图,已知四边形ABCD的直观图是直角梯形A1B1C1D1,且A1B1=B1C1=2A1D1=4,则四边形ABCD的面积为( )
如图,已知四边形ABCD的直观图是直角梯形A1B1C1D1,且A1B1=B1C1=2A1D1=4,则四边形ABCD的面积为( )| A. | 12 | B. | 12$\sqrt{2}$ | C. | 24$\sqrt{2}$ | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com