
分析 利用向量数量积运算性质、夹角公式即可得出.
解答 解:∵向量$\overrightarrow{a}$=(-1,0),$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
∴$|\overrightarrow{a}|$=1,$|\overrightarrow{b}|$=$\sqrt{(\frac{1}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}$=1,
$\overrightarrow{a}•\overrightarrow{b}$=-$\frac{1}{2}$.
∴$cos<\overrightarrow{a},\overrightarrow{b}>$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{-\frac{1}{2}}{1×1}$=-$\frac{1}{2}$,
则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 本题考查了向量数量积运算性质、夹角公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
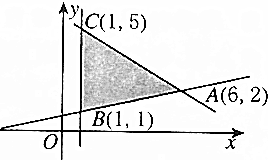 给出平面可行域(如图),若使目标函数z=ax+y取最大值的最优解有无穷多个,则a=( )
给出平面可行域(如图),若使目标函数z=ax+y取最大值的最优解有无穷多个,则a=( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | 4 | D. | $\frac{5}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com