
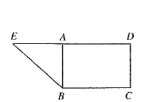
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,
上一点,![]() ,现沿
,现沿![]() 将
将![]() 折起到
折起到![]() 的位置,并使
的位置,并使![]() 平面
平面![]() ,点
,点![]() 在
在![]() 边上,且满足
边上,且满足![]() .
.
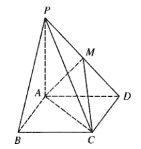
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,求二面角
,求二面角![]() 的大小.
的大小.
 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 为椭圆
为椭圆![]() 的右焦点,且椭圆
的右焦点,且椭圆![]() 上的点到
上的点到![]() 的距离的最小值为
的距离的最小值为![]() ,过
,过![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点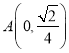 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在这样的直线![]() ,使得以
,使得以![]() ,
,![]() 为邻边的平行四边形为矩形?若存在,求出直线
为邻边的平行四边形为矩形?若存在,求出直线![]() 的斜率;若不存在,请说明理由.
的斜率;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种新型嫁接巨丰葡萄,在新疆地区种植一般亩产不低于5千斤,产量高的达到上万斤.受嫁接年限的影响,其产量一般逐年衰减,若在新疆地区平均亩产量低于5千斤,则从新嫁接.以下是新疆某地区从2014年开始嫁接后每年的平均亩产量y(单位:千斤)的数据表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号x | 1 | 2 | 3 | 4 | 5 |
平均亩产量y | 8.2 | 7.8 | 7.2 | 6.6 | 5.4 |
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归直线方程,预计哪一年开始从新嫁接.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: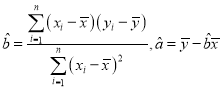 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为贯彻落实党中央全面建设小康社会的战略部署,某贫困地区的广大党员干部深入农村积极开展“精准扶贫”工作.经过多年的精心帮扶,截至2018年底,按照农村家庭人均年纯收入8000元的小康标准,该地区仅剩部分家庭尚未实现小康.现从这些尚未实现小康的家庭中随机抽取50户,得到这50户家庭2018年的家庭人均年纯收入的频率分布直方图,如图.
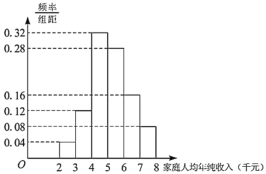
注:在频率分布直方图中,同一组数据用该区间的中点值作代表.
(1)估计该地区尚未实现小康的家庭2018年家庭人均年纯收入的平均值;
(2)2019年7月,为估计该地能否在2020年全面实现小康,收集了当地最贫困的一户家庭2019年1至6月的人均月纯收入的数据,作出散点图如下.
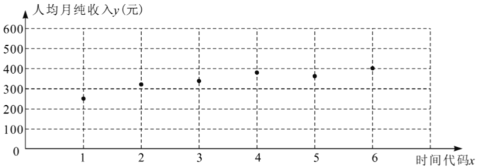
根据相关性分析,发现其家庭人均月纯收入![]() 与时间代码
与时间代码![]() 之间具有较强的线性相关关系(记2019年1月、2月……分别为
之间具有较强的线性相关关系(记2019年1月、2月……分别为![]() ,
,![]() ,…,依此类推).试预测该家庭能否在2020年实现小康生活.
,…,依此类推).试预测该家庭能否在2020年实现小康生活.
参考数据:![]() ,
,![]() .
.
参考公式:线性回归方程![]() 中,
中, ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为该椭圆的一条垂直于
为该椭圆的一条垂直于![]() 轴的动弦,直线
轴的动弦,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)证明:点![]() 恒在椭圆
恒在椭圆![]() 上.
上.
(2)设直线![]() 与椭圆
与椭圆![]() 只有一个公共点
只有一个公共点![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,在平面内是否存在定点
,在平面内是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出该点坐标;若不存在,说明理由.
恒成立?若存在,求出该点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为F,上顶点为A,直线AF与直线
的左焦点为F,上顶点为A,直线AF与直线![]() 垂直,垂足为B,且点A是线段BF的中点.
垂直,垂足为B,且点A是线段BF的中点.
(I)求椭圆C的方程;
(II)若M,N分别为椭圆C的左,右顶点,P是椭圆C上位于第一象限的一点,直线MP与直线![]() 交于点Q,且
交于点Q,且![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com