Question

【题目】已知关于的不等式.

（1）不等式的解集为，求实数的值；

（2）在（1）的条件下，求不等式的解集；

（3）解关于的不等式.

Answer 1

【答案】（1）；（2）；（3）见解析.

【解析】

（1）根据不等式的解与对应的方程的根的关系结合韦达定理可求实数的值.

（2）移项通分后可把分式不等式转化为一元二次不等式，注意分母不为零.

（3）就五种情形分类讨论可得不等式的解.

（1）因为不等式的解集为，

所以为的两个根，所以，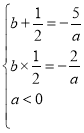

解得，故.

（2）由（1）得即为，故，

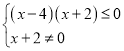所以，所以，故原不等式的解集为.

（3）不等式等价于，

整理得到：.

当时，不等式的解为.

当时，不等式的解为.

当时，，故不等式的解为.

当时，，不等式的解为.

当时，，故不等式的解为.

综上，当时，不等式的解为；当时，不等式的解为；

当时，不等式的解为；当时，不等式的解为；

当时，不等式的解为.