练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一条光线从点射出,经轴反射后与圆相交于点,且,求反射光线所在的直线方程.

    【答案】和.

    【解析】试题分析：当反射光线的斜率不存在时，反射光线所在的直线方程为；当反射光线的斜率存在时,设反射光线直线方程，利用点到直线的距离公式，求解的值，即可得到直线的方程.

    试题解析：

    点关于轴的对称点为,

    ()当反射光线的斜率不存在时,反射光线所在的直线方程为: ,

    此时,圆心到反射光线的距离为,且圆的半径为,

    所以反射光线被圆所截得的弦长,符合题意.

    ()当反射光线的斜率存在时,设反射光线的斜率为,则反射光线所在的直线方程为即.

    因为反射光线被圆所截得的弦长,且圆的半径为,

    所以圆心到反射光线的距离为.

    而圆心到反射光线的距离,

    即,解得.

    所以反射光线所在的直线方程为即.

    综上,反射光线所在的直线方程为和.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图所示，已知抛物线C：y2＝4x的焦点为F，直线l经过点F且与抛物线C相交于A、B两点．

    (1)若线段AB的中点在直线y＝2上，求直线l的方程；

    (2)若线段|AB|＝20，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)对任意x，y∈R，都有f(x＋y)＝f(x)＋f(y)，且x＞0时，f(x)＜0， f(1)＝－2.

    (1)求证:f(x)是奇函数；

    (2)判断函数的单调性

    (3)求f(x)在[－3,3]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法正确的个数有（ ）

    ①用刻画回归效果，当越大时，模型的拟合效果越差；反之，则越好；

    ②可导函数在处取得极值，则；

    ③归纳推理是由特殊到一般的推理，而演绎推理是由一般到特殊的推理；

    ④综合法证明数学问题是“由因索果”，分析法证明数学问题是“执果索因”.

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图程序框图的算法思路源于我国古代数学名著《九章算术》中的某一种算法．执行该程序框图，输入分别为98，63，则输出的结果是（ ）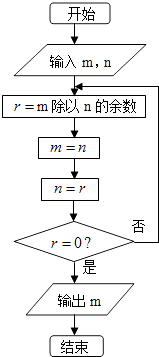

    A.14
    B.18
    C.9
    D.7

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年1曰8日，中共中央、国务院隆重举行国家科学技术奖励大会，在科技界引发热烈反响，自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料，由大数据测得该产品的性能指标值与这种新材料的含量（单位：克）的关系为：当时， 是的二次函数；当时， .测得数据如表（部分）

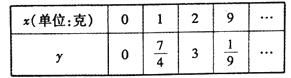
    （1）求关于的函数关系式；

    （2）其函数的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方体中，点在上运动，给出下列四个命题：

    ①三棱锥的体积不变； ②；

    ③平面； ④平面平面；

    其中正确的命题是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在上的函数满足条件，且函数是偶函数，当时， ；当时， 的最小值为，则＝（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|a﹣3x|﹣|2+x|．
    （1）若a=2，解不等式f（x）≤3；
    （2）若存在实数a，使得不等式f（x）≥1﹣a+2|2+x|成立，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案