
【题目】下列说法正确的个数有( )
①用 刻画回归效果,当
刻画回归效果,当![]() 越大时,模型的拟合效果越差;反之,则越好;
越大时,模型的拟合效果越差;反之,则越好;
②可导函数![]() 在
在![]() 处取得极值,则
处取得极值,则![]() ;
;
③归纳推理是由特殊到一般的推理,而演绎推理是由一般到特殊的推理;
④综合法证明数学问题是“由因索果”,分析法证明数学问题是“执果索因”.
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】用相关指数![]() 来刻画回归效果,
来刻画回归效果, ![]() 值越大,说明模型的拟合效果越好,故①错误;
值越大,说明模型的拟合效果越好,故①错误;
根据极值的定义可知, 可导函数![]() 在
在![]() 处取得极值,则
处取得极值,则![]() 正确;
正确;
归纳推理是由部分到整体,特殊到一般的推理,演绎推理是由一般到特殊的推理,故③正确;
根据综合法的定义可得,综合法是执因导果,是顺推法,根据分析法的定义可得,分析法是执果索因,是直接证法,是逆推法,故④正确;
综上可得,正确的个数为3个,故选C.
点睛:本题考查的是推理的定义与辨析,属于基础题.推理分为合情推理和演绎推理,其中合情推理又分为归纳推理和类比推理两个部分.判断一个推理的过程是否是演绎推理的关键,是看题意是否符合演绎推理的定义,即能否从推理过程中找出”三段论”的三个组成部分.


科目:高中数学 来源: 题型:
【题目】已知命题p:曲线C:(m+2)x2+my2=1表示双曲线,命题q:方程y2=(m2﹣1)x表示的曲线是焦点在x轴的负半轴上的抛物线,若p∨q为真命题,p∧q为假命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2x的定义域是[2,16].设g(x)=f(2x)﹣[f(x)]2.
(1)求函数g(x)的解析式及定义域;
(2)求函数g(x)的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)=(﹣x2+ax﹣3)ex(a为实数).
(1)当a=4时,求函数y=g(x)在x=0处的切线方程;
(2)求f(x)在区间[t,t+2](t>0)上的最小值;
(3)如果关于x的方程g(x)=2exf(x)在区间[ ![]() ,e]上有两个不等实根,求实数a的取值范围.
,e]上有两个不等实根,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)判断函数的奇偶性,并加以证明;
(2)用定义证明![]() 在
在![]() 上是减函数;
上是减函数;
(3)函数![]() 在
在![]() 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为调查高二学生上学路程所需要的时间(单位:分钟),从高二年级学生中随机抽取![]() 名按上学所需要时间分组:第
名按上学所需要时间分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
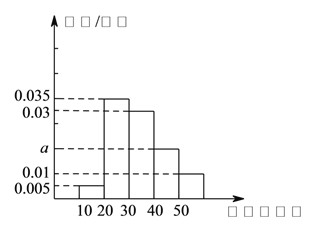
(![]() )根据图中数据求
)根据图中数据求![]() 的值.
的值.
(![]() )若从第
)若从第![]() ,
, ![]() ,
, ![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名新生参与交通安全问卷调查,应从第
名新生参与交通安全问卷调查,应从第![]() ,
, ![]() ,
, ![]() 组各抽取多少名新生?
组各抽取多少名新生?
(![]() )在(
)在(![]() )的条件下,该校决定从这
)的条件下,该校决定从这![]() 名学生中随机抽取
名学生中随机抽取![]() 名新生参加交通安全宣传活动,求第
名新生参加交通安全宣传活动,求第![]() 组至少有一志愿者被抽中的概率.
组至少有一志愿者被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com