
【题目】如图,正方体![]() 中,点
中,点![]() 在
在![]() 上运动,给出下列四个命题:
上运动,给出下列四个命题:
①三棱锥![]() 的体积不变; ②
的体积不变; ②![]() ;
;
③![]() 平面
平面![]() ; ④平面
; ④平面![]() 平面
平面![]() ;
;
其中正确的命题是__________.

【答案】①③④
【解析】分析: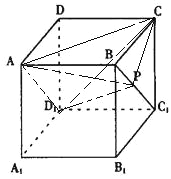 ①V A-D1PC=V C-AD1P,C到面 AD1P的距离不变,且三角形 AD1P的面积不变.
①V A-D1PC=V C-AD1P,C到面 AD1P的距离不变,且三角形 AD1P的面积不变.
②,当P 与B重合时,DP与BC1;成60°角,不垂直.
③连接A1B,A1C1容易证明平面BA1C1∥面ACD1,从而由线面平行的定义可得;
④连接DB1,容易证明DB1⊥面ACD1 ,从而可以证明面面垂直.
解答: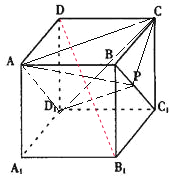 解:对于①,V A-D1PC=V C-AD1P,C到面 AD1P的距离不变,且三角形 AD1P的面积不变.∴三棱锥A-D1PC的体积不变; 正确;
解:对于①,V A-D1PC=V C-AD1P,C到面 AD1P的距离不变,且三角形 AD1P的面积不变.∴三棱锥A-D1PC的体积不变; 正确;
②连接DB,DC1,可知△DBC1是正三角形,当且仅当P为BC1中点时,DP⊥BC1,考虑特殊位置,当P 与B重合时,DP与BC1成60°角,不垂直.
错误
③连接A1B,A1C1容易证明平面BA1C1∥面ACD1,从而由线面平行的定义可得 A1P∥平面ACD1;.正确.
④连接DB1,根据正方体的性质,有DB1⊥面ACD1 ,DB1?平面PDB1 从而可以证明平面PDB1⊥ACD1;正确.
正确的命题个数有 3个.
故选C.


科目:高中数学 来源: 题型:
【题目】甲,乙两名工人加工同一种零件,两人每天加工的零件数相同,所得次品数分别为![]() ,
,![]() ,
,![]() 和
和![]() 的分布列如下表.
的分布列如下表.

(![]() )分别求期望
)分别求期望![]() 和
和![]() .
.
(![]() )试对这两名工人的技术水平进行比较.
)试对这两名工人的技术水平进行比较.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)=(﹣x2+ax﹣3)ex(a为实数).
(1)当a=4时,求函数y=g(x)在x=0处的切线方程;
(2)求f(x)在区间[t,t+2](t>0)上的最小值;
(3)如果关于x的方程g(x)=2exf(x)在区间[ ![]() ,e]上有两个不等实根,求实数a的取值范围.
,e]上有两个不等实根,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,平面
为正方形,平面![]() 底面
底面![]() ,
, ![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() 平面
平面![]() ;
;
(Ⅲ)在棱![]() 上求作一点
上求作一点![]() ,使得
,使得![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2分别是双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左右焦点,若在双曲线的右支上存在一点M,使得(
=1(a>0,b>0)的左右焦点,若在双曲线的右支上存在一点M,使得( ![]() +
+ ![]() )
) ![]() =0(其中O为坐标原点),且|
=0(其中O为坐标原点),且| ![]() |=
|= ![]() |
| ![]() |,则双曲线离心率为 .
|,则双曲线离心率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x2﹣2ax+b|(x∈R),给出下列命题:
①a∈R,使f(x)为偶函数;
②若f(0)=f(2),则f(x)的图象关于x=1对称;
③若a2﹣b≤0,则f(x)在区间[a,+∞)上是增函数;
④若a2﹣b﹣2>0,则函数h(x)=f(x)﹣2有2个零点.
其中正确命题的序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com