练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图,在四棱锥中,底面为正方形,平面底面, ,点分别是的中点.

    （Ⅰ）求证: 平面;

    （Ⅱ）求证: 平面;

    （Ⅲ）在棱上求作一点,使得,并说明理由.

    【答案】（Ⅰ）见解析；（Ⅱ）见解析；（Ⅲ）见解析.

    【解析】试题分析：（Ⅰ）证明即可得到平面

    （Ⅱ）证明和即可证明平面

    （Ⅲ）取中点，连接， ，过点作，交于点. 则点即为所求作的点.

    试题解析：（Ⅰ）因为点， 分别是， 的中点，所以

    因为四边形为正方形，所以

    所以

    因为平面， 平面，

    所以平面

    （Ⅱ）因为平面底面， ，

    所以平面

    因为平面，所以

    因为，点是的中点，所以

    因为， 平面， 平面，

    所以平面

    （Ⅲ）取中点，连接， ，过点作，交于点. 则点即为所求作的点.

    理由：因为，点是的中点，所以

    因为平面底面，所以平面

    所以

    因为， ，所以平面

    因为平面，所以

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= ﹣mx（m∈R）．
    （1）当m=0时，求函数f（x）的零点个数；
    （2）当m≥0时，求证：函数f（x）有且只有一个极值点；
    （3）当b＞a＞0时，总有 ＞1成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义：如果函数在定义域内给定区间上存在，满足 ，则称函数是上的“平均值函数”，是它的均值点.

    （1）是否是上的“平均值函数”，如果是请找出它的均值点；如果不是，请说明理由；

    （2）现有函数是上的平均值函数，则求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图程序框图的算法思路源于我国古代数学名著《九章算术》中的某一种算法．执行该程序框图，输入分别为98，63，则输出的结果是（ ）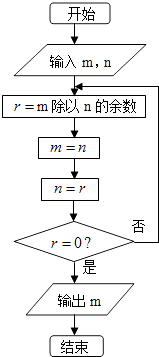

    A.14
    B.18
    C.9
    D.7

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知两条不同直线、，两个不同平面、，给出下列命题：

    ①若垂直于内的两条相交直线，则⊥；

    ②若∥，则平行于内的所有直线；

    ③若 ， 且⊥，则⊥；

    ④若 ，，则⊥；

    ⑤若 ， 且∥，则∥；

    其中正确命题的序号是__________________．（把你认为正确命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方体中，点在上运动，给出下列四个命题：

    ①三棱锥的体积不变； ②；

    ③平面； ④平面平面；

    其中正确的命题是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知AD、BE、CF分别是△ABC三边的高，H是垂心，AD的延长线交△ABC的外接圆于点G．

    （1）求证：∠CHG=∠ABC；
    （2）求证：ABGD=ADHC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，则f（f（-1））=______；不等式f（x）≥1的解集为______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了了解某地高一学生的体能状况，某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图），图中从左到右各小长方形的面积之比为2：4：17：15：9：3，第二小组频数为12．

    （1）第二小组的频率是多少？样本容量是多少？

    （2）若次数在110以上为达标，试估计全体高一学生的达标率为多少？

    （3）通过该统计图，可以估计该地学生跳绳次数的众数是______，中位数是_______.

    查看答案和解析>>

    同步练习册答案