练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在三棱柱中，侧面底面，，，，为的中点.

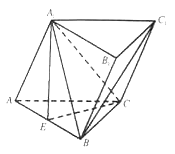
    （1）求证：平面；

    （2）求证：平面；

    （3）求三棱锥的体积.

    【答案】（1）证明见解析；（2）证明见解析；（3）.

    【解析】分析：（1）连接，设，利用三角形中位线定理可得，由线面平行的判定定理可得结论；（2）由勾股定理可得，，利用面面垂直的性质可得平面，从而可得，利用线面垂直的判定定理可得结论；（3）因为平面，平面，所以，利用棱锥的体积公式可得结果.

    详解：（1）连接，设，则为的中点.

    因为为的中点，

    所以.

    又平面， ，

    所以平面.

    （2）证明：在中，由，，，得，即；

    在中，同理可得.

    因为侧面底面，侧面底面，

    所以平面.

    又平面，

    所以，

    又，

    所以平面.

    （3）因为平面，平面，

    所以.

    在直角中，由及，得.

    所以 .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某学生对其30位亲属的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主).

    (1)根据茎叶图,帮助这位同学说明这30位亲属的饮食习惯.

    (2)根据以上数据完成如下2×2列联表.

    (3)能否有99％的把握认为其亲属的饮食习惯与年龄有关?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，平面平面，四边形为矩形， ，点为的中点.

    (1)证明： 平面.

    (2)点为上任意一点，在线段上是否存在点，使得？若存在，确定点的位置，并加以证明；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，且cos2 ﹣sinBsinC= ．
    （1）求A；
    （2）若a=4，求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直三棱柱ABC﹣A′B′C′中，AA′=2AC=2BC，E为AA′的中点，C′E⊥BE．

    （1）求证：C′E⊥平面BCE；
    （2）求直线AB′与平面BEC′所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ln（2ax+1）+ ﹣x2﹣2ax（a∈R）．
    （1）若x=2为f（x）的极值点，求实数a的值；
    （2）若y=f（x）在[3，+∞）上为增函数，求实数a的取值范围；
    （3）当a=﹣ 时，方程f（1﹣x）= 有实根，求实数b的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC－A1B1C1中，已知AC⊥BC，BC＝CC1，设AB1的中点为D，B1C∩BC1＝E.

    求证：(1)DE∥平面AA1C1C；

    (2)BC1⊥AB1.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题共13分）

    以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊，无法确认，在图中经X表示。

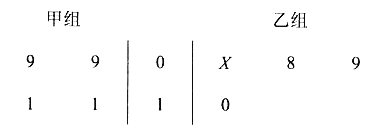
    （Ⅰ）如果X=8，求乙组同学植树棵数的平均数和方差；

    （Ⅱ）如果X=9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率。

    （注：方差其中为，，的平均数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】把函数f（x）= 图象上各点向右平移（＞0）个单位，得到函数g（x）=sin2x的图象，则的最小值为 ．

    查看答案和解析>>

    同步练习册答案