练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知，，分别为的中点，，将沿折起，得到四棱锥，为的中点.

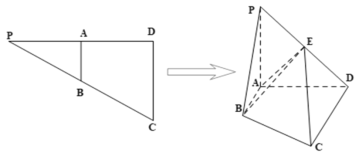
    （1）证明：平面；

    （2）当正视图方向与向量的方向相同时，此时的正视图的面积为，求四棱锥的体积.

    【答案】（1）证明见解析；（2）

    【解析】

    （1）根据题意可知，由三线合一可证明，进而由线面垂直的判定可证明平面；

    （2）根据平面平面，所以在平面内的射影应该落在直线上，所以点到平面的距离为，进一步求出点到平面的距离，然后代入锥体体积公式计算即可.

    解：（1）由平面图可知，，，，

    所以平面，所以.

    因为为的中点，，∴.

    因为，所以平面.

    （2）因为的正视图与全等，所以，

    ∴，∴或.

    由（1）可知，平面平面，所以在平面内的射影应该落在直线

    上，所以点到平面的距离为，

    所以四棱锥的体积.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设首项为a1的正项数列{an}的前n项和为Sn，q为非零常数，已知对任意正整数n，m，Sn+m＝Sm+qmSn总成立．

    （1）求证：数列{an}是等比数列；

    （2）若不等的正整数m，k，h成等差数列，试比较ammahh与ak2k的大小；

    （3）若不等的正整数m，k，h成等比数列，试比较与的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图在三棱锥中，和均为等腰三角形，且，．

    （1）判断是否成立？并给出证明；

    （2）求直线与平面所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于的不等式，对于恒成立，则实数的取值范围是________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一，为坚决打赢脱贫攻坚战，某帮扶单位考察了甲乙两种不同的农产品加工生产方式，现对两种生产方式加工的产品质量进行测试并打分对比，得到如下数据：

    生产方式甲

    分值区间

    频数

    20

    30

    100

    40

    10

    生产方式乙

    分值区间

    频数

    25

    35

    60

    50

    30

    其中产品质量按测试指标可划分为：指标在区间上的为特优品，指标在区间上的为一等品，指标在区间上的为二等品．

    （1）用事件表示“按照生产方式甲生产的产品为特优品”，估计的概率；

    （2）填写下面列联表，并根据列联表判断能否有的把握认为“特优品”与生产方式有关？

    特优品

    非特优品

    生产方式甲

    生产方式乙

    （3）根据打分结果对甲乙两种生产方式进行优劣比较．

    附表：

    0.10

    0.050

    0.010

    0.001

    2.706

    3.841

    6.635

    10.828

    参考公式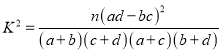：，其中．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在多面体中，是等边三角形，是等腰直角三角形， ，平面平面，平面.

    (1) 求证：；

    (2) 若，求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，已知椭圆的离心率为，且过点. 为椭圆的右焦点， 为椭圆上关于原点对称的两点，连接分别交椭圆于两点.

    ⑴求椭圆的标准方程；

    ⑵若，求的值；

    ⑶设直线， 的斜率分别为， ，是否存在实数，使得，若存在，求出的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝xlnx，函数g（x）＝kx﹣cosx在点处的切线平行于x轴.

    （1）求函数f（x）的极值；

    （2）讨论函数F（x）＝g（x）﹣f（x）的零点的个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，焦距为，直线过椭圆的左焦点.

    （1）求椭圆的标准方程；

    （2）若直线与轴交于点是椭圆上的两个动点,的平分线在轴上,.试判断直线是否过定点，若过定点，求出定点坐标;若不过定点，请说明理由.

    查看答案和解析>>

    同步练习册答案