
【题目】已知点![]() 在椭圆
在椭圆![]() :
:![]() (
(![]() )上,且点
)上,且点![]() 到左焦点
到左焦点![]() 的距离为3.
的距离为3.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 关于坐标原点
关于坐标原点![]() 的对称点为
的对称点为![]() ,又
,又![]()
![]() 两点在椭圆
两点在椭圆![]() 上,且
上,且![]() ,求凸四边形
,求凸四边形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由题意点![]() 到左焦点
到左焦点![]() 的距离为3,结合两点间距离公式可求得
的距离为3,结合两点间距离公式可求得![]() 的值,将点
的值,将点![]() 代入椭圆,根据椭圆中
代入椭圆,根据椭圆中![]() 的关系式即可求得
的关系式即可求得![]() ,进而得椭圆的标准方程.
,进而得椭圆的标准方程.
(2)由![]() 可设直线
可设直线![]() 的方程为
的方程为![]() ,联立椭圆方程,整理变形根据两个交点可令
,联立椭圆方程,整理变形根据两个交点可令![]() 求得
求得![]() 的范围.设
的范围.设![]()
![]() ,由韦达定理表示出
,由韦达定理表示出![]() ,
,![]() ,由弦长公式求得
,由弦长公式求得![]() ,点到直线距离公式求得
,点到直线距离公式求得![]() 到
到![]() 的距离,结合
的距离,结合![]() 用
用![]() 表示出
表示出![]() ,令
,令![]() ,可化简为
,可化简为![]() ,再令
,再令![]() ,利用导函数求得
,利用导函数求得![]() 的单调性和最值,即可求解.
的单调性和最值,即可求解.
(1)因为椭圆![]() 经过点
经过点![]() ,所以
,所以![]() .
.
设左焦点![]() (
(![]() ),
),
则由![]() 得
得![]() ,
,
解得![]() .
.
又![]() ,于是
,于是![]() ,
,
解得![]() (舍负),
(舍负),
进而![]() .
.
故椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)因为![]() ,可设直线
,可设直线![]() 的方程为
的方程为![]() (
(![]() ),
),
联立 并整理得
并整理得![]() .
.
由![]() ,解得
,解得![]() .
.
设![]()
![]() ,则
,则![]() ,
,![]() .
.
所以![]()
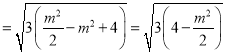 .
.
又![]() 与
与![]() 之间的距离即
之间的距离即![]() 到
到![]() 的距离
的距离![]() ,且
,且![]() .
.
所以四边形![]() 的面积
的面积 .
.
设![]() ,由
,由![]() 可得
可得![]() ,
,
则![]() ,
,
记之为函数![]() ,则
,则![]() ,
,
易知![]() 在区间
在区间![]() 内单调递增,在区间
内单调递增,在区间![]() 内单调递减.
内单调递减.
故![]() 的最大值为
的最大值为![]() ,此时
,此时![]() ,解得
,解得![]() ,符合题意,
,符合题意,
所以四边形![]() 面积的最大值为
面积的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:![]() )和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用水量 | [0,0.1) | [0.1,0.2) | [0.2,0.3) | [0.3,0.4) | [0.4,0.5) | [0.5,0.6) | [0.6,0.7) |
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 | [0,0.1) | [0.1,0.2) | [0.2,0.3) | [0.3,0.4) | [0.4,0.5) | [0.5,0.6) |
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)作出使用了节水龙头50天的日用水量数据的频率分布直方图;
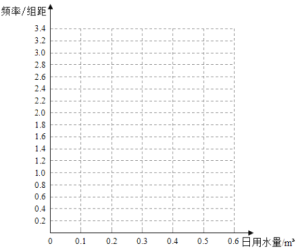
(2)估计该家庭使用节水龙头后,日用水量小于0.3![]() 的概率;
的概率;
(3)估计该家庭用节水龙头后,一年能节省多少水.(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某厂的某种产品400件,经质检,其中有一等品252件、二等品100件、三等品40件、次品8件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为![]() .
.
(1)求![]() 的分布列和1件产品的平均利润(即
的分布列和1件产品的平均利润(即![]() 的期望);
的期望);
(2)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.如果此时要求1件产品的平均利润不小于4.75万元,则三等品率最多是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某控制器中有一个易损部件,现统计了30个该部件的使用寿命,结果如下(单位:小时);
710 721 603 615 760 742 841 591 590 721 718 750 760 713 709
681 736 654 722 732 722 715 726 699 755 751 709 733 705 700
(1)估计该部件的使用寿命达到一个月及以上的概率(一个月按30天计算);
(2)为了保证该控制器能稳定工作,将若干个同样的部件按下图连接在一起组成集成块,每一个部件是否能正常工作互不影响.对比![]() 和
和![]() 时,哪个能保证集成块使用寿命达到一个月及以上的概率超过0.8?
时,哪个能保证集成块使用寿命达到一个月及以上的概率超过0.8?
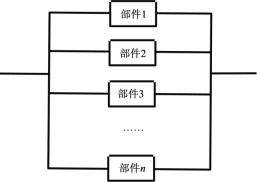
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为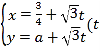 为参数
为参数![]() ,圆C的标准方程为
,圆C的标准方程为![]() 以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
![]() 求直线l和圆C的极坐标方程;
求直线l和圆C的极坐标方程;
![]() 若射线
若射线![]() 与l的交点为M,与圆C的交点为A,B,且点M恰好为线段AB的中点,求a的值.
与l的交点为M,与圆C的交点为A,B,且点M恰好为线段AB的中点,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年5月20日以来,广东自西北到东南出现了一次明显降雨.为了对某地的降雨情况进行统计,气象部门对当地20日~28日9天内记录了其中100小时的降雨情况,得到每小时降雨情况的频率分布直方图如下:
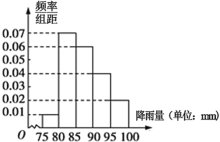
若根据往年防汛经验,每小时降雨量在![]() 时,要保持二级警戒,每小时降雨量在
时,要保持二级警戒,每小时降雨量在![]() 时,要保持一级警戒.
时,要保持一级警戒.
(1)若以每组的中点代表该组数据值,求这100小时内每小时的平均降雨量;
(2)若从记录的这100小时中按照警戒级别采用分层抽样的方法抽取10小时进行深度分析.再从这10小时中随机抽取3小时,求抽取的这3小时中属于一级警戒时间的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com