Question

11．在平行六面体ABCD-EFGH中，若$\overrightarrow{AG}$=x$\overrightarrow{AB}$-2y$\overrightarrow{BC}$+3z$\overrightarrow{DH}$，则x+y+z等于（　　）

• A． $\frac{7}{6}$
• B． $\frac{2}{3}$
• C． $\frac{5}{6}$
• D． 1

Answer 1

分析 在平行六面体ABCD-EFGH中，$\overrightarrow{AG}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CG}$，结合$\overrightarrow{AG}$=x$\overrightarrow{AB}$-2y$\overrightarrow{BC}$+3z$\overrightarrow{DH}$，$\overrightarrow{CG}$=$\overrightarrow{DH}$，求出x，y，z，即可得出结论．

解答 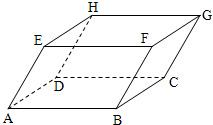解：在平行六面体ABCD-EFGH中，$\overrightarrow{AG}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CG}$，
∵$\overrightarrow{AG}$=x$\overrightarrow{AB}$-2y$\overrightarrow{BC}$+3z$\overrightarrow{DH}$，$\overrightarrow{CG}$=$\overrightarrow{DH}$，
∴x=1，-2y=1，3z=1，
∴$x=1，y=-\frac{1}{2}$，z=$\frac{1}{3}$，
∴x+y+z=$\frac{5}{6}$，
故选：C．

点评 考查向量加法的平行四边形法则，空间向量的加法运算，比较基础．