
分析 (1)列举出所有的可能的数对,由分步计数原理知共有10个,看清要求满足的条件,写出所有的数对,要做到不重不漏.
(2)设事件“f(x)=ax2-6bx+1在区间[1,+∞)上为增函数”为B,因函数f(x)=ax2-6bx+1的图象的对称轴为为x=$\frac{3b}{a}$且a>0,所以要使事件B发生,只需$\frac{3b}{a}$≤1,即3b≤a,写出所有的满足条件的数对.
解答 解:(1)所有基本事件如下:
(2,-1),(2,1),(2,2),(2,3),(2,4),
(3,-1),(3,1),(3,2),(3,3),(3,4),共有10个.
设事件“a≥2,且b≤3”为A,
则事件A包含的基本事件有8个,
所以P(A)=$\frac{8}{10}$=0.8.
(2)设事件“f(x)=ax2-6bx+1在区间[1,+∞)上为增函数”为B,
因函数f(x)=ax2-6bx+1的图象的对称轴为x=$\frac{3b}{a}$且a>0,
所以要使事件B发生,只需$\frac{3b}{a}$≤1,即3b≤a.
由满足题意的数对有(2,-1)、(3,-1)、(3,1),共3个,
∴P(B)=$\frac{3}{10}$=0.3.
点评 本题主要考查古典概型,考查学生的计算能力,列举出所有事件是关键.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{x^2}$,g(x)=($\sqrt{x}$)2 | B. | f(x)=1,g(x)=x0 | ||
| C. | f(x)=$\root{3}{x^3}$,g(x)=x | D. | f(x)=x-1,g(x)=$\frac{{{x^2}-1}}{x+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(a+b)(\frac{1}{a}+\frac{1}{b})≥4$ | B. | a3+b3≥2ab | C. | a2+b2≥2a+2b | D. | $\sqrt{|{a-b}|}$≤$|\sqrt{a}-\sqrt{b}|$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
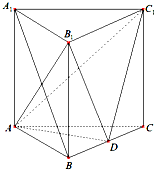 如图,正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,D是BC的中点.
如图,正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,D是BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com