
【题目】为了研究学生的数学核心素养与抽象能力(指标![]() )、推理能力(指标
)、推理能力(指标![]() )、建模能力(指标
)、建模能力(指标![]() )的相关性,将它们各自量化为1、2、3三个等级,再用综合指标
)的相关性,将它们各自量化为1、2、3三个等级,再用综合指标![]() 的值评定学生的数学核心素养,若
的值评定学生的数学核心素养,若![]() ,则数学核心素养为一级;若
,则数学核心素养为一级;若![]() ,则数学核心素养为二级;若
,则数学核心素养为二级;若![]() ,则数学核心素养为三级,为了了解某校学生的数学核心素养,调查人员随机访问了某校10名学生,得到如下数据:
,则数学核心素养为三级,为了了解某校学生的数学核心素养,调查人员随机访问了某校10名学生,得到如下数据:
学生编号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)在这10名学生中任取两人,求这两人的建模能力指标相同条件下综合指标值也相同的概率;
(2)在这10名学生中任取三人,其中数学核心素养等级是一级的学生人数记为![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望.
的分布列及其数学期望.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为别为
的左、右焦点为别为![]() 、
、![]() ,且过点
,且过点![]() 和
和![]() .
.
(1)求椭圆的标准方程;
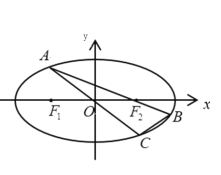
(2)如图,点![]() 为椭圆上一动点(非长轴端点),
为椭圆上一动点(非长轴端点),![]() 的延长线与椭圆交于点
的延长线与椭圆交于点![]() ,
,![]() 的延长线与椭圆交于点
的延长线与椭圆交于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 为圆
为圆![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上的投影为
轴上的投影为![]() ,动点
,动点![]() 满足
满足![]() ,动点
,动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,过点
,过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,
,![]() 与
与![]() 交于另一点为
交于另一点为![]() .若以点
.若以点![]() 为圆心,以线段
为圆心,以线段![]() 长为半径的圆与
长为半径的圆与![]() 有4个公共点,求
有4个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数:f(x)=x2﹣mx﹣n(m, n∈R).
(1)若m+n=0,解关于x的不等式f(x)≥x(结果用含m式子表示);
(2)若存在实数m,使得当x∈[1,2]时,不等式x≤f(x)≤4x恒成立,求实数n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的参数方程是
的参数方程是 (m>0,t为参数),曲线
(m>0,t为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与曲线
,与曲线![]() 交于点
交于点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作,它问世后不久便风行宇内,成为明清之际研习数学者必读的教材,而且传到朝鲜、日本及东南亚地区,对推动汉字文化圈的数学发展起了重要的作用.卷八中第33问是:“今有三角果一垛,底阔每面七个,问该若干?”如图是解决该问题的程序框图,执行该程序框图,求得该垛果子的总数![]() 为( )
为( )

A. 120 B. 84 C. 56 D. 28
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学进行篮球三分球投篮比赛,甲每次投中的概率为![]() ,乙每次投中的概率为
,乙每次投中的概率为![]() ,每人分别进行三次投篮.
,每人分别进行三次投篮.
(I)记甲投中的次数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(Ⅱ)求乙至多投中2次的概率;
(Ⅲ)求乙恰好比甲多投进2次的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com