
【题目】设点![]() 为圆
为圆![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上的投影为
轴上的投影为![]() ,动点
,动点![]() 满足
满足![]() ,动点
,动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,过点
,过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,
,![]() 与
与![]() 交于另一点为
交于另一点为![]() .若以点
.若以点![]() 为圆心,以线段
为圆心,以线段![]() 长为半径的圆与
长为半径的圆与![]() 有4个公共点,求
有4个公共点,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() ,
, ![]() 分别为椭圆的上顶点和右焦点,
分别为椭圆的上顶点和右焦点, ![]() 的面积为
的面积为![]() ,直线
,直线![]() 与椭圆交于另一个点
与椭圆交于另一个点![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(1)求直线![]() 的斜率;
的斜率;
(2)设平行于![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,
, ![]() ,且与直线
,且与直线![]() 交于点
交于点![]() ,求证:存在常数
,求证:存在常数![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆的中心为原点O,长轴在x轴上,离心率![]() ,过左焦点F1作x轴的垂线交椭圆于A,
,过左焦点F1作x轴的垂线交椭圆于A,![]() 两点
两点![]() .
.
(Ⅰ)求该椭圆的标准方程;
(Ⅱ)取垂直于x轴的直线与椭圆相交于不同的两点P,![]() ,过P、
,过P、![]() 作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若
作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若![]() ,求圆Q的标准方程.
,求圆Q的标准方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】11月11日有2000名网购者在某购物网站进行网购消费(金额不超过1000元),其中女性1100名,男性900名.该购物网站为优化营销策略,根据性别采用分层抽样的方法从这2000名网购者中抽取200名进行分析,如表.(消费金额单位:元)

(1)计算![]() 的值,在抽出的200名且消费金额在
的值,在抽出的200名且消费金额在![]() 的网购者中随机抽出2名发放网购红包,求选出的2人均为女性的概率;
的网购者中随机抽出2名发放网购红包,求选出的2人均为女性的概率;
(2)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上数据列![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“是否为网购达人与性别有关?”附:
的把握认为“是否为网购达人与性别有关?”附:![]() ,
,![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行了一次“环保知识竞赛”活动. 为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为![]() )进行统计. 按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).
)进行统计. 按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).
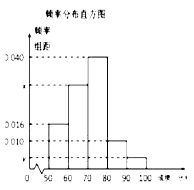

(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() ,
,![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动,设![]() 表示所抽取的3名同学中得分在[80,90)的学生人数,求
表示所抽取的3名同学中得分在[80,90)的学生人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提高黔东南州的整体旅游服务质量,州旅游局举办了黔东南州旅游知识竞赛,参赛单位为本州内各旅游协会,参赛选手为持证导游.现有来自甲旅游协会的导游3名,其中高级导游2名;乙旅游协会的导游5名,其中高级导游3名.从这8名导游中随机选择4人 参加比赛.
(Ⅰ)设![]() 为事件“选出的4人中恰有2名高级导游,且这2名高级导游来自同一个旅游协会”,求事件
为事件“选出的4人中恰有2名高级导游,且这2名高级导游来自同一个旅游协会”,求事件![]() 发生的概率.
发生的概率.
(Ⅱ)设![]() 为选出的4人中高级导游的人数,求随机变量
为选出的4人中高级导游的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)在极坐标系下,设曲线![]() 与射线
与射线![]() 和射线
和射线![]() 分别交于
分别交于![]() ,
,![]() 两点,求
两点,求![]() 的面积;
的面积;
(2)在直角坐标系下,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com