
 ijУ�ӲμӸ���ģ�⿼�Ե�ѧ���������ȡ60��ѧ����������ѧ�ɼ�����Ϊ90����150��֮����������ֳ�����[90��100����[100��110��������[140��150����õ����²���Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�ε���Ϣ���ش��������⣺
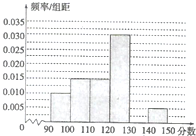
ijУ�ӲμӸ���ģ�⿼�Ե�ѧ���������ȡ60��ѧ����������ѧ�ɼ�����Ϊ90����150��֮����������ֳ�����[90��100����[100��110��������[140��150����õ����²���Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�ε���Ϣ���ش��������⣺���� ��1������Ƶ�ʷֲ�ֱ��ͼ�ĸ�С�����ε����֮��Ϊ1�����������[130��140���ڵ�Ƶ�ʣ�
��2����Ƶ�ʷֲ�ֱ��ͼ�����ƽ���֣�
��3�������[110��120����[120��130�������ε��������÷ֲ�����ķ����ڸ��������ڳ�ȡ��������������������������ȡ2�ˣ���ǡ����2���ڷ�����[120��130���ڡ����ʼ��ɣ�
��� �⣺��1��������[130��140���ڵ�Ƶ��Ϊ
1-10����0.01+0.015+0.015+0.030+0.005��=1-0.75=0.25��
��2������ƽ����Ϊ$\overline{x}$=95��0.1+105��0.15+115��0.15+125��0.3+135��0.25+145��0.05=121��
��3�������⣬[110��120�������ε�����Ϊ60��0.15��=9���ˣ���[120��130�������ε�����Ϊ60��0.3=18���ˣ���
���÷ֲ�����ķ����ڷ�����Ϊ[110��130����ѧ���г�ȡһ������Ϊ6��������
������[110��120���������ڳ�ȡ2�ˣ����ֱ��Ϊm��n����[120��130���������ڳ�ȡ4�ˣ����ֱ��Ϊa��b��c��d��
�衰����������ȡ2�ˣ�ǡ����2���ڷ�����[120��130���ڡ�Ϊ�¼�A��
������¼��У�m��n������m��a������m��b������m��c������m��d������n��a������n��b������n��c������n��d������a��b������a��c������a��d������b��c������b��d������c��d����15�֣�
���¼�A�����Ļ����¼��У�a��b������a��c������a��d������b��c������b��d������c��d����6�֣�
��P��A��=$\frac{6}{15}$=$\frac{3}{5}$��
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ��Ӧ���Լ��ֲ�����ŵ���͵ļ������⣬����ʱӦ���оٷ���������¼��ĸ������Ӷ�����������⣬���ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | $\frac{1}{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
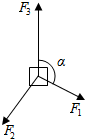 ��ͼ��һ������ˮƽ���ڵ�������F1��F2��F3�������±���ƽ�⣬���F1=5N��F2=7N���Ϧ�=120�㣬��F3=8N��
��ͼ��һ������ˮƽ���ڵ�������F1��F2��F3�������±���ƽ�⣬���F1=5N��F2=7N���Ϧ�=120�㣬��F3=8N���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
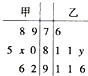 ij��ѧ��һ���Ӽס����������и�ѡ��7��ѧ���μ���ѧ����������ȡ�õijɼ�������100�֣��ľ�Ҷͼ��ͼ�����мװ�ѧ���ɼ���������80���Ұ�ѧ���ɼ�����λ����89����x+y��ֵΪ��������
ij��ѧ��һ���Ӽס����������и�ѡ��7��ѧ���μ���ѧ����������ȡ�õijɼ�������100�֣��ľ�Ҷͼ��ͼ�����мװ�ѧ���ɼ���������80���Ұ�ѧ���ɼ�����λ����89����x+y��ֵΪ��������| A�� | 7 | B�� | 8 | C�� | 9 | D�� | 14 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $y=sin��-2x-\frac{2��}{3}��$ | B�� | $y=sin��-2x+\frac{2��}{3}��$ | C�� | $y=sin��-2x-\frac{��}{3}��$ | D�� | $y=sin��-2x+\frac{��}{3}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com