
分析 2a=3,可得a=log23=$\frac{lg3}{lg2}$,又log35=b=$\frac{lg5}{lg3}$,可得lg3=alg2,lg5=blg3=balg2.代入log1520=$\frac{2lg2+lg5}{lg3+lg5}$即可得出.
解答 解:∵2a=3,∴a=log23=$\frac{lg3}{lg2}$,又log35=b=$\frac{lg5}{lg3}$,
∴lg3=alg2,lg5=blg3=balg2.
则log1520=$\frac{2lg2+lg5}{lg3+lg5}$=$\frac{2lg2+ablg2}{alg2+ablg2}$=$\frac{2+ab}{a+ab}$.
故答案为:$\frac{2+ab}{a+ab}$.
点评 本题考查了指数与对数的运算法则,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| P(K2>k0) | 0.50 | 0.10 | 0.05 | 0.01 | 0.001 |
| k0 | 0.455 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一次函数 | B. | 二次函数 | C. | 指数函数 | D. | 对数函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
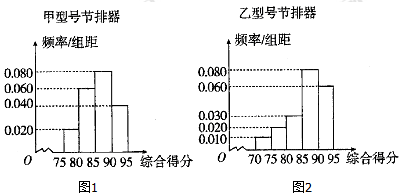
| 综合得分k的范围 | 节排器等级 | 节排器利润率 |
| k≥85 | 一级品 | a |
| 75≤k<85 | 二级品 | 5a2 |
| 70≤k<75 | 三级品 | a2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com