
设函数f(x)=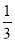 x3-ax(a>0),g(x)=bx2+2b﹣1.
x3-ax(a>0),g(x)=bx2+2b﹣1.
(1)若曲线y=f(x)与y=g(x)在它们的交点(1,c)处有相同的切线,求实数a,b的值;
(2)当b=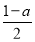 时,若函数h(x)=f(x)+g(x)在区间(﹣2,0)内恰有两个零点,求实数a的取值范围;
时,若函数h(x)=f(x)+g(x)在区间(﹣2,0)内恰有两个零点,求实数a的取值范围;
(3)当a=1,b=0时,求函数h(x)=f(x)+g(x)在区间[t,t+3]上的最小值.
(1)a= ,b=
,b= ;(2)(0,
;(2)(0, );(3)[h(x)]min=
);(3)[h(x)]min= .
.
【解析】试题分析:(1)求出f'(x),g'(x),由题意得f(1)=g(1),且f'(1)=g'(1),解该方程组即可;(2)记h(x)=f(x)+g(x),当a=1-2b时,h(x)= ,利用导数可研究其单调性、极值情况,由函数在(-2,0)内有两零点可得端点处函数值及极值符号,由此得一不等式组,解出即可;(3)a=1,b=0时,h(x)=f(x)+g(x)=
,利用导数可研究其单调性、极值情况,由函数在(-2,0)内有两零点可得端点处函数值及极值符号,由此得一不等式组,解出即可;(3)a=1,b=0时,h(x)=f(x)+g(x)=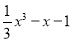 ,由(2)可知,函数h(x)的单调区间及极值点,按照在区间[t,t+3]内没有极值点,一个极值点,两个极值点分类讨论,结合图象及函数的单调性即可求得其最大值
,由(2)可知,函数h(x)的单调区间及极值点,按照在区间[t,t+3]内没有极值点,一个极值点,两个极值点分类讨论,结合图象及函数的单调性即可求得其最大值
试题解析:(1)因为f(x)=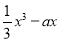 ,g(x)=bx2+2b﹣1,
,g(x)=bx2+2b﹣1,
所以f′(x)=x2﹣a,g′(x)=2bx.
因为曲线y=f(x)与y=g(x)在它们的交点(1,c)处有相同切线,
所以f(1)=g(1),且f′(1)=g′(1).
即 -a=b+2b-1,且1﹣a=2b,
-a=b+2b-1,且1﹣a=2b,
解得a= ,b=
,b= .
.
(2)当a=1﹣2b时,h(x)= (a>0),
(a>0),
所以h′(x)=x2+(1﹣a)x﹣a=(x+1)(x﹣a).
令h′(x)=0,解得x1=﹣1,x2=a>0.
当x变化时,h′(x),h(x)的变化情况如下表:
x (﹣∞,﹣1) ﹣1 (﹣1,a) a (a,+∞)
h′(x) + 0 ﹣ 0 +
h(x) ↗ 极大值 ↘ 极小值 ↗
所以函数h(x)的单调递增区间为(﹣∞,﹣1),(a,+∞),单调递减区间为(﹣1,a).
故h(x)在区间(﹣2,﹣1)内单调递增,在区间(﹣1,0)内单调递减.
从而函数h(x)在区间(﹣2,0)内恰有两个零点,当且仅当
即 解得:0<a<
解得:0<a< .
.
所以实数a的取值范围是(0, ).
).
(3)当a=1,b=0时,h(x)=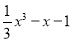 .
.
所以函数h(x)的单调递增区间为(﹣∞,﹣1),(1,+∞),单调递减区间为(﹣1,1).
由于h(-2)=- ,h(1)=-
,h(1)=- ,所以h(﹣2)=h(1).
,所以h(﹣2)=h(1).
①当t+3<1,即t<﹣2时,
[h(x)]min=h(t)= t3-t-1
t3-t-1
②当﹣2≤t<1时,[h(x)]min=h(1)=- .
.
③当t≥1时,h(x)在区间[t,t+3]上单调递增,[h(x)]min=h(t)= t3-t-1.
t3-t-1.
综上可知,函数h(x)在区间[t,t+3]上的最小值为
[h(x)]min= .
.
考点:利用导数研究曲线上某点切线方程;函数的零点;利用导数求闭区间上函数的最值


科目:高中数学 来源: 题型:
| A、2x-y-1=0 |
| B、2x+y-1=0 |
| C、x-2y-1=0 |
| D、2x-y+1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 3 |
| π |
| 3 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 1 |
| ρ12 |
| 1 |
| ρ22 |
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试文科数学试卷(解析版) 题型:选择题
设p:(x-2)(y-5)≠0;q:x≠2或y≠5,则p是q的( )条件
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:选择题
已知命题:p:对任意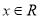 ,总有
,总有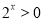 ;q:“x>1”是“x>2”的充分不必要条件.
;q:“x>1”是“x>2”的充分不必要条件.
则下列命题为真命题的是( )
A.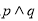 B.
B. C.
C.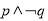 D.
D.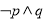
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:解答题
在△ABC中,已知∠A=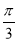 ,边BC=2
,边BC=2 ,设∠B=x,△ABC的周长记为y.
,设∠B=x,△ABC的周长记为y.
(1)求函数y=f(x)的解析式,并指出其定义域;
(2)求函数y=f(x)的单调区间及其值域.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:选择题
设x∈R,若函数f(x)为单调递增函数,且对任意实数x,都有f[f(x)-ex]=e+1(e是自然对数的底数),则f(ln2)的值等于( )
A.1 B.e+1 C.3 D.e+3
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考理科数学试卷(解析版) 题型:填空题
无重复数字的五位数a1a2a3a4a5 , 当a1<a2, a2>a3, a3<a4, a4>a5时称为波形数,则由1,2,3,4,5任意组成的一个没有重复数字的五位数是波形数的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com