
设x∈R,若函数f(x)为单调递增函数,且对任意实数x,都有f[f(x)-ex]=e+1(e是自然对数的底数),则f(ln2)的值等于( )
A.1 B.e+1 C.3 D.e+3
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:解答题
已知点P(x1,y1),Q(x2,y2)是函数f(x)=sin(ωx+Φ)(ω>0,0<Φ<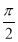 )图象上的任意两点,若|y1-y2|=2时,|x1-x2|的最小值为
)图象上的任意两点,若|y1-y2|=2时,|x1-x2|的最小值为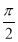 ,且函数f(x)的图象经过点(0,2),在△ABC中,角A,B,C的对边分别为a,b,c,且2sinAsinC+cos2B=1.
,且函数f(x)的图象经过点(0,2),在△ABC中,角A,B,C的对边分别为a,b,c,且2sinAsinC+cos2B=1.
(1)求函数f(x)的解析式;
(2)求g(B)=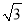 f(B)+f(B+
f(B)+f(B+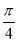 )的取值范围.
)的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:解答题
如图,在四棱柱ABCD—A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2 CD=2,M是线段AB的中点.
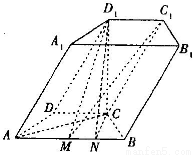
(1)求证:C1M∥平面A1ADD1 ;
(2)若CD1垂直于平面ABCD且CD1=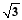 ,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:解答题
设函数f(x)=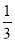 x3-ax(a>0),g(x)=bx2+2b﹣1.
x3-ax(a>0),g(x)=bx2+2b﹣1.
(1)若曲线y=f(x)与y=g(x)在它们的交点(1,c)处有相同的切线,求实数a,b的值;
(2)当b=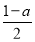 时,若函数h(x)=f(x)+g(x)在区间(﹣2,0)内恰有两个零点,求实数a的取值范围;
时,若函数h(x)=f(x)+g(x)在区间(﹣2,0)内恰有两个零点,求实数a的取值范围;
(3)当a=1,b=0时,求函数h(x)=f(x)+g(x)在区间[t,t+3]上的最小值.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:填空题
已知O为坐标原点,点M(3,2),若N(x,y)满足不等式组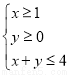 ,则
,则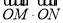 的最大值为 _________ .
的最大值为 _________ .
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:选择题
已知三个数2,m,8构成一个等比数列,则圆锥曲线 的离心率为( )
的离心率为( )
A.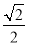 B.
B.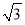 C.
C.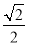 或
或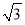 D.
D.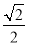 或
或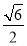
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考理科数学试卷(解析版) 题型:解答题
某公司计划在迎春节联欢会中设一项抽奖活动:在一个不透明的口袋中装入外形一样号码分别为1,2,3, ,10的十个小球.活动者一次从中摸出三个小球,三球号码有且仅有两个连号的为三等奖,奖金30元;三球号码都连号为二等奖,奖金60元;三球号码分别为1,5,10为一等奖,奖金240元;其余情况无奖金.
(1)求员工甲抽奖一次所得奖金ξ的分布列与期望;
(2)员工乙幸运地先后获得四次抽奖机会,他得奖次数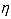 的方差是多少?
的方差是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com