
某公司计划在迎春节联欢会中设一项抽奖活动:在一个不透明的口袋中装入外形一样号码分别为1,2,3, ,10的十个小球.活动者一次从中摸出三个小球,三球号码有且仅有两个连号的为三等奖,奖金30元;三球号码都连号为二等奖,奖金60元;三球号码分别为1,5,10为一等奖,奖金240元;其余情况无奖金.
(1)求员工甲抽奖一次所得奖金ξ的分布列与期望;
(2)员工乙幸运地先后获得四次抽奖机会,他得奖次数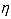 的方差是多少?
的方差是多少?
(1)分布列见解析,Eξ=20;(2)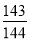
【解析】试题分析:(1)先分别求出ξ=30,60,240的概率,然后利用对立事件概率之和为1,可以求得ξ=0的概率,从而写出分布列和期望;(2)四次抽奖,每一次获奖概率相同,属于独立重复试验,用二项分布方法处理。
试题解析:(1)甲抽奖一次,基本事件总数为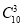 =120,奖金ξ的所有可能取值为0,30,60,240.
=120,奖金ξ的所有可能取值为0,30,60,240.
一等奖的情况只有一种,所以奖金为240元的概率为P(ξ=240)=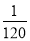
三球连号的情况有1,2,3;2,3,4; 8,9,10共8种,所以P(ξ=60)= 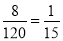
仅有两球连号中,对应1,2与9,10的各有7种;对应2,3;3,4; 8,9各有6种.
得奖金30的概率为P(ξ=30)=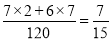
奖金为0的概率为P(ξ=0)=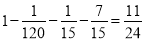
ξ的分布列为:
ξ | 0 | 30 | 60 | 240 |
P |
|
|
|
|
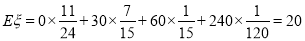 6分
6分
(2) 由(1)可得乙一次抽奖中中奖的概率为P=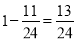 10分
10分
四次抽奖是相互独立的, 所以中奖次数η~B(4,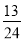 )故
)故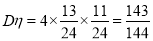 .12分
.12分
考点:概率,随机变量分布列与期望


科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:选择题
在△ABC中,三内角A,B,C成等差数列,b=6,则△ABC的外接圆半径为( )
A.6 B.12 C.2 D.4
D.4
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:选择题
已知命题:p:对任意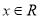 ,总有
,总有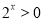 ;q:“x>1”是“x>2”的充分不必要条件.
;q:“x>1”是“x>2”的充分不必要条件.
则下列命题为真命题的是( )
A.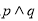 B.
B. C.
C.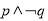 D.
D.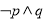
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:选择题
设x∈R,若函数f(x)为单调递增函数,且对任意实数x,都有f[f(x)-ex]=e+1(e是自然对数的底数),则f(ln2)的值等于( )
A.1 B.e+1 C.3 D.e+3
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:选择题
下列判断错误的是( )
A.平行于同一条直线的两条直线互相平行
B.平行于同一平面的两个平面互相平行
C.经过两条异面直线中的一条,有且仅有一个平面与另一条直线平行
D.垂直于同一平面的两个平面互相平行
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考理科数学试卷(解析版) 题型:填空题
无重复数字的五位数a1a2a3a4a5 , 当a1<a2, a2>a3, a3<a4, a4>a5时称为波形数,则由1,2,3,4,5任意组成的一个没有重复数字的五位数是波形数的概率为 .
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考理科数学试卷(解析版) 题型:选择题
若(9x-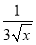 )n(n∈N*)的展开式中第3项的二项式系数为36,则其展开式中的常数项为( )
)n(n∈N*)的展开式中第3项的二项式系数为36,则其展开式中的常数项为( )
A.84 B.-252 C.252 D.-84
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com